题目内容
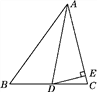
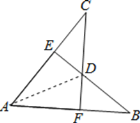
【题目】如图,AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D.有下列结论:
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠BAC的平分线上;④CF是AB的垂直平分线.以上结论正确的有( )个.
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
由∠A=∠A,AB=AC,∠B=∠C,可推出①选项正确;由AE=AF,AD=AD可知②正确;由∠B=∠C,BF=CE,可证得△BDF≌△CDE,得到③正确;而点F不一定是AB的中点,故④错误.
:∵BE⊥AC于E,CF⊥AB于F,
∴∠AFC=∠AEB=90°,故在Rt△AEB中,∠B=90°-∠A,在Rt△AFC中∠C=90°-∠A,
∴∠B=∠C,
在△ABE和△ACF中,
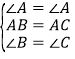 ,
,
∴△ABE≌△ACF(ASA),
故①选项正确,
由AE=AF,AC=AB,得BF=CE,
在△BDF和△CDE中,
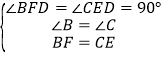 ,
,
∴△BDF≌△CDE,选项②正确,
∵△ABE≌△ACF,
∴AE=AF,AC=AB,
连接AD,
在Rt△AFD和Rt△AED中,
![]() ,
,
∴Rt△AFD≌Rt△AED(HL),
∴∠DAF=∠DAE,即点D在∠BAC的平分线上,选项③正确,
而点F不一定是AB的中点,故④错误.
故选:C.

【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术饰品 | a | 2 | 90 |
电热水壶 | 35 | 1 | b |
合计 | 8 | 280 | |
(1)直接写出a= ,b= ;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术饰品和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?
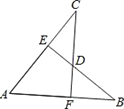
【题目】如图,AD是△ABC的角平分线,过点D向AB,AC两边作垂线,垂足分别为E,F,那么下列结论中不一定正确的是( )

A. BD=CD B. DE=DF C. AE=AF D. ∠ADE=∠ADF
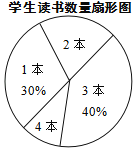
【题目】某校七年级共有500名学生,在“世界读书日”前夕,开展了“阅读助我成长”的读书活动.为了解该年级学生在此次活动中课外阅读情况,童威随机抽取m名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如下统计表和扇形图.
学生读书数量统计表
阅读量/本 | 学生人数 |
1 | 15 |
2 | a |
3 | b |
4 | 5 |
(1)直接写出m、a、b的值;
(2)估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本?