题目内容
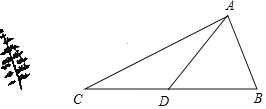
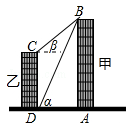
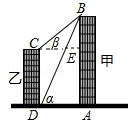
【题目】如图,线段AB、CD分别表示甲乙两建筑物的高,BA⊥AD,CD⊥DA,垂足分别为A、D.从D点测到B点的仰角α为60°,从C点测得B点的仰角β为30°,甲建筑物的高AB=30米
(1)求甲、乙两建筑物之间的距离AD.
(2)求乙建筑物的高CD.
【答案】(1)![]() ;(2)20.
;(2)20.
【解析】
(1)在Rt△ABD中利用三角函数即可求解;
(2)作CE⊥AB于点E,在Rt△BCE中利用三角函数求得BE的长,然后根据CD=AE=AB﹣BE求解.
(1)作CE⊥AB于点E,在Rt△ABD中,AD=![]() =
=![]() =
=![]() (米);
(米);
(2)在Rt△BCE中,CE=AD=![]() 米,BE=CEtanβ=
米,BE=CEtanβ=![]() ×
×![]() =10(米),则CD=AE=AB﹣BE=30﹣10=20(米)
=10(米),则CD=AE=AB﹣BE=30﹣10=20(米)
答:乙建筑物的高度DC为20m.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
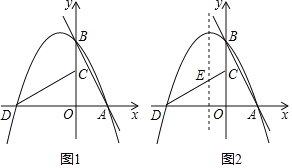
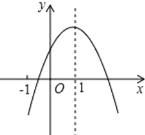
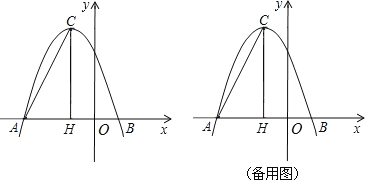
【题目】抛物线![]() 中,函数值y与自变量
中,函数值y与自变量![]() 之间的部分对应关系如下表:
之间的部分对应关系如下表:
| … |
|
|
| 0 | 1 | … |
y | … |
|
| 0 |
|
| … |
(1)求该抛物线的表达式;
(2)如果将该抛物线平移,使它的顶点移到点M(2,4)的位置,那么其平移的方法是____________.