题目内容
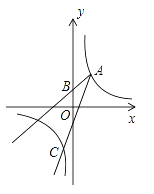
【题目】如图①，直线l：y＝mx+n（m＜0，n＞0）与x、y轴分别相交于A、B两点，将△AOB绕点O逆时针旋转90°得到△COD，过点A、B、D的抛物线P叫做l的关联抛物线，而l叫做P的关联直线．
（1）若l：y＝﹣2x+2，则P表示的函数解析式为 ；若P：y＝﹣x2﹣3x+4，则l表示的函数解析式为 ．
（2）求P的对称轴（用含m、n的代数式表示）；
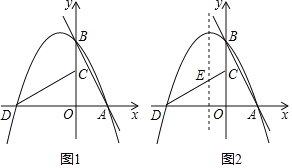
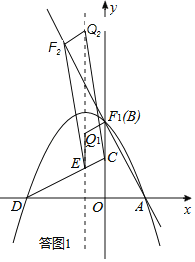
（3）如图②，若l：y＝﹣2x+4，P的对称轴与CD相交于点E，点F在l上，点Q在P的对称轴上．当以点C，E，Q，F为顶点的四边形是以CE为一边的平行四边形时，求点Q的坐标．
【答案】（1）y＝﹣x2﹣x+2；y＝﹣4x+4；（2）
；（3）满足条件的点Q坐标为
、
．
【解析】
（1）若l：y=-2x+2，求出点A、B、D的坐标，利用待定系数法求出P表示的函数解析式；若P：y=-x2-3x+4，求出点D、A、B的坐标，再利用待定系数法求出l表示的函数解析式；
（2）根据对称轴的定义解答即可；
（3）以点C，E，Q，F为顶点的四边形是以CE为一边的平行四边形时，则有FQ∥CE，且FQ=CE．以此为基础，列方程求出点Q的坐标．
解：（1）若l：y＝﹣2x+2，则A（1，0），B（0，2）．
∵将△AOB绕点O逆时针旋转90°，得到△COD，
∴D（﹣2，0）．
设P表示的函数解析式为：y＝ax2+bx+c，将点A、B、D坐标代入得：
，
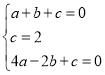解得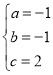
，
∴P表示的函数解析式为：y＝﹣x2﹣x+2；
若P：y＝﹣x2﹣3x+4＝﹣（x+4）（x﹣1），
则D（﹣4，0），A（1，0）．
∴B（0，4）．
设l表示的函数解析式为：y＝kx+b，将点A、B坐标代入得：
，解得
，
∴l表示的函数解析式为：y＝﹣4x+4．
故答案为：y＝﹣x2﹣x+2；y＝﹣4x+4．
（2）直线l：y＝mx+n，（m＜0，n＞0）与x、y轴分别相交于A、B两点，
∴
，B（0，n），D（﹣n，0）．
设抛物线对称轴与x轴的交点为N（x，0）．
∵DN＝AN．
∴
，
∴
，
∴p的对称轴为．
（3）l：y＝﹣2x+4，
当x=0时，y=4；当y=0时，x=2，
∴A（2，0）、B（0，4）．
∵OC=OA,OD=OB,
∴C（0，2），D（﹣4，0）．
设yCD=k1x+b1,
∴
,
∴
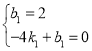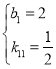
∴直线CD的解析式为：
．
由（2）可得，p的对称轴为x＝﹣1．
∵以点C、E、Q、F为顶点的四边形是以CE为一边的平行四边形．
∴FQ∕∕CE，且FQ＝CE．
设直线FQ的解析式为：
．
∵点E、点C的横坐标相差1．
∴点F、点Q的横坐标也是相差1．
则|xF﹣（﹣1）|＝|xF+1|＝1．
解得xF＝0或xF＝﹣2．
∵点F在直线l1：y＝﹣2x+4上．
∴点F坐标为（0，4）或（﹣2，8）．
若F（0，4），
∴b=4,
∴直线FQ的解析式为：
．
当x＝﹣1时，
．
∴．
若F（﹣2，8），
∴8=-1+b,
∴b=9,
∴直线FQ的解析式为：
．
当x＝﹣1时，
，
∴．
∴满足条件的点Q坐标为、．
