题目内容
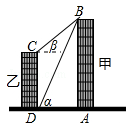
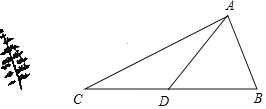
【题目】某校一棵大树发生一定的倾斜，该树与地面的夹角∠ABC＝75°．小明测得某时大树的影子顶端在地面C处，此时光线与地面的夹角∠ACB＝30°；又过了一段时间，测得大树的影子顶端在地面D处，此时光线与地面的夹角∠ADB＝50°．若CD＝8米，求该树倾斜前的高度（即AB的长度）．（结果保留一位小数．参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19，sin75°≈0.97，cos75°≈0.26，tan75°≈3.73，
≈1.73）
【答案】该树倾斜前的高度是10.6米．
【解析】
过A作AHLBC于H，然后多次使用锐角三角函数即可求解.
解：如图：过A作AH⊥BC于H，
在Rt△ACH中，∵∠C＝30°，
∴tan30°＝
，
∴CH＝
＝
AH，
在Rt△ADH中，
∵∠ADH＝45°，
∴DH＝AH，
∵CD＝CH﹣DH＝AH﹣AH＝8，
∴AH＝
＝4（+1），
在Rt△AHB中，
∵∠B＝75°，
∴sin75°＝
，
∴AB＝AHsin75°＝4（+1）×0.97≈10.6米，
答：该树倾斜前的高度是10.6米．
练习册系列答案
相关题目
