题目内容
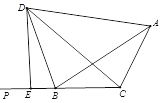
【题目】如图,BD是△ABC的外角∠ABP的角平分线,DA=DC,DE⊥BP于点E,若AB=5,BC=3,则BE的长为 _____________
【答案】1
【解析】
过点D作DF⊥AB于F,根据角平分线上的点到角的两边的距离相等可得DE=DF,再利用“HL”证明△BDE和△BDF全等,△ADF和△CDE全等,根据全等三角形对应边相等可得BE=BF,AF=CE,再用AB、BC表示出AF、CE,整理即可解得.
如图,过点D作DF⊥AB于F,
∵BD是∠ABP的角平分线,
∴DE=DF,
在△BDE和△BDF中,![]()
∴△BDE≌△BDF(HL),
∴BE=BF,
在△ADF和△CDE中,![]()
∴△ADF≌△CDE(HL),
∴AF=CE,
∵AF=ABBF,
CE=BC+BE,
∴ABBF=BC+BE,
∴2BE=ABBC,
∵AB=5,BC=3,
∴2BE=53=2,
解得BE=1.
故答案为:1.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目