题目内容
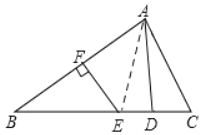
【题目】如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,D为线段CE的中点,BE=AC.
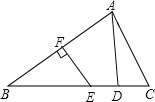
(1)求证:AD⊥BC.
(2)若∠BAC=75°,求∠B的度数.
【答案】(1)详见解析,(2)35°.
【解析】
(1)连接AE,根据垂直平分线的性质,可知BE=AE=AC,根据等腰三角形三线合一即可知AD⊥BC
(2)设∠B=x°,由(1)可知∠BAE=∠B=x°,然后根据三角形ABC的内角和为180°列出方程即可求出x的值.
(1)连接AE,
∵EF垂直平分AB,
∴AE=BE,
∵BE=AC,
∴AE=AC,
∵D是EC的中点,
∴AD⊥BC;
(2)设∠B=x°,
∵AE=BE,
∴∠BAE=∠B=x°,
∴由三角形的外角的性质,∠AEC=2x°,
∵AE=AC,
∴∠C=∠AEC=2x°,
在三角形ABC中,3x°+75°=180°,
x°=35°,
∴∠B=35°.

练习册系列答案
相关题目