题目内容
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.
(1)求此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
(4)连接AC,H是抛物线上一动点,过点H作AC的平行线交x轴于点F.是否存在这样的点F,使得以A,C,H,F为顶点所组成的四边形是平行四边形?若存在,求出满足条件的点F的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),
∴OB=3,
∵OC=OB,
∴OC=3,
∴c=3,C(0,3),
将A(1,0)、B(﹣3,0)代入y=ax2+bx+3中,
得: ![]() ,解得:
,解得: ![]() .
.
∴所求抛物线解析式为:y=﹣x2﹣2x+3.
(2)
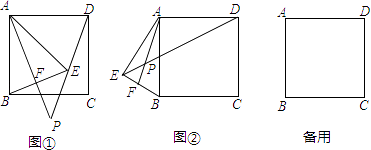
解:如图1,过点E作EF⊥x轴于点F,
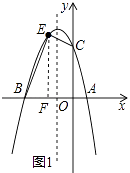
设E(m,﹣m2﹣2m+3)(﹣3<m<0),
∴EF=﹣m2﹣2m+3,BF=m+3,OF=﹣m,
∴S四边形BOCE= ![]() BFEF+
BFEF+ ![]() (OC+EF)OF,
(OC+EF)OF,
= ![]() (m+3)(﹣m2﹣2m+3)+
(m+3)(﹣m2﹣2m+3)+ ![]() (﹣m2﹣2m+3+3)(﹣a),
(﹣m2﹣2m+3+3)(﹣a),
=﹣ ![]() m2﹣
m2﹣ ![]() m+
m+ ![]() ,
,
=﹣ ![]() +
+ ![]() .
.
∵a=﹣ ![]() <0,
<0,
∴当m=﹣ ![]() 时,S四边形BOCE最大,且最大值为
时,S四边形BOCE最大,且最大值为 ![]() ,
,
此时点E的坐标为(﹣ ![]() ,
, ![]() ).
).
(3)
解:设点P的坐标为(﹣1,n),如图2,过A1作A1N⊥对称轴于N,设对称轴与x轴交于点M.
①当n>0时,∵∠NP1A1+∠MP1A=∠NA1P1+∠NP1A1=90°,
∴∠NA1P1=∠MP1A,
在△A1NP1与△P1MA中,  ,
,
∴△A1NP1≌△P1MA(AAS),
∴A1N=P1M=n,P1N=AM=2,
∴A1(n﹣1,n+2),
将A1(n﹣1,n+2)代入y=﹣x2﹣2x+3得:n+2=﹣(x﹣1)2﹣2(n﹣1)+3,
解得:n=1,n=﹣2(舍去),
此时P1(﹣1,1);
②当n<0时,要使P2A=P2A2,由图可知A2点与B点重合,
∵∠AP2A2=90°,
∴MP2=MA=2,
∴P2(﹣1,﹣2),
∴满足条件的点P的坐标为P(﹣1,1)或(﹣1,﹣2).
(4)
解:假设存在,设点F的坐标为(t,0),
以A,C,H,F为顶点的平行四边形分两种情况(如图3):

①当点H在x轴上方时,
∵A(1,0),C(0,3),F(t,0),
∴H(t﹣1,3),
∵点H在抛物线y=﹣x2﹣2x+3上,
∴3=﹣(t﹣1)2﹣2(t﹣1)+3,
解得:t1=﹣1,t2=1(舍去),
此时F(﹣1,0);
②当点H在x轴下方时,
∵A(1,0),C(0,3),F(t,0),
∴H(t+1,﹣3),
∵点H在抛物线y=﹣x2﹣2x+3上,
∴﹣3=﹣1(t+1)2﹣2(t+1)+3,
解得:t3=﹣2﹣ ![]() ,t4=﹣2+
,t4=﹣2+ ![]() ,
,
此时F(﹣2﹣ ![]() ,0)或(﹣2+
,0)或(﹣2+ ![]() ,0).
,0).
综上可知:存在这样的点F,使得以A,C,H,F为顶点所组成的四边形是平行四边形,点F的坐标为(﹣1,0)、(﹣2﹣ ![]() ,0)或(﹣2+
,0)或(﹣2+ ![]() ,0).
,0).
【解析】(1)由点B的坐标可知OB的长,根据OC=OB,即可得出点C的坐标以及c,再根据点A、B的坐标利用待定系数法即可求出二次函数解析式;(2)过点E作EF⊥x轴于点F,设E(m,﹣m2﹣2m+3)(﹣3<m<0),结合B、O、C点的坐标即可得出BF、OF、OC、EF的长,利用分割图形求面积法即可找出S四边形BOCE关于m的函数关系式,利用配方法以及二次函数的性质即可解决最值问题;(3)设点P的坐标为(﹣1,n),过A1作A1N⊥对称轴于N,设对称轴与x轴交于点M.分n>0和n<0考虑:①当n>0时,利用相等的边角关系即可证出△A1NP1≌△P1MA(AAS),由此即可得出点A1的坐标,将其代入二次函数解析式中即可求出n值,由此即可得出点P1的坐标;②当n<0时,结合图形找出点A2的位置,由此即可得出点P2的坐标.综上即可得出结论;(4)假设存在,设点F的坐标为(t,0),分点H在x轴上方和下方两种情况考虑,根据平行四边形的性质结合A、C、F点的坐标即可表示出点H的坐标,将其代入二次函数解析式中即可求出t值,从而得出点F的坐标.
【考点精析】利用二次函数的图象对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,有下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴是x=1;
③抛物线与x轴有两个交点,它们之间的距离是 ![]() ;
;
④在对称轴左侧y随x增大而增大.
其中正确的说法是( )
A.①②③
B.②③④
C.②③
D.①④