题目内容
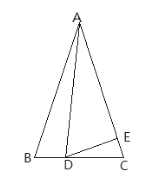
【题目】如图,点O是等边△ABC内一点.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.已知∠AOB=110°.

(1)求证:△COD是等边三角形;
(2)当α=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当α为多少度时,△AOD是等腰三角形.
【答案】(1)证明见解析;(2)△AOD是直角三角形.理由见解析;(3)125°,或110°,或140°.
【解析】
试题分析:此题有一定的开放性,要找到变化中的不变量才能有效解决问题.
试题解析:(1)∵CO=CD,∠OCD=60°,
∴△COD是等边三角形;
(2)当α=150°,即∠BOC=150°时,△AOD是直角三角形.
∵△BOC≌△ADC,
∴∠ADC=∠BOC=150°,
又∵△COD是等边三角形,
∴∠ODC=60°,
∴∠ADO=90°,
即△AOD是直角三角形;
(3)①要使AO=AD,需∠AOD=∠ADO.
∵∠AOD=360°-∠AOB-∠COD-α=360°-110°-60°-α=190°-α,∠ADO=α-60°,
∴190°-α=α-60°
∴α=125°;
②要使OA=OD,需∠OAD=∠ADO.
∵∠AOD=190°-α,∠ADO=α-60°,
∴∠OAD=180°-(∠AOD+∠ADO)=50°,
∴α-60°=50°
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD.
∵190°-α=50°
∴α=140°.
综上所述:当α的度数为125°,或110°,或140°时,△AOD是等腰三角形.

练习册系列答案
相关题目