题目内容
如图,已知抛物线 与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
(1)求抛物线的函数表达式;
(2)设P为对称轴上一动点,求△APC周长的最小值;
(3)设D为抛物线上一点,E为对称轴上一点,若以点A,B,D,E为顶点的四边形是菱形,则点D的坐标为 .
解:(1)∵AB=2,对称轴为直线x=2,
∴点A的坐标是(1,0),点B的坐标是(3,0)。
设抛物线的函数表达式为 ,
,
将A(1,0)代入得: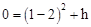 ,解得
,解得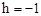 。
。
∴抛物线的函数表达式为 ,即
,即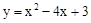 。
。
(2)如图1,连接AC、BC,BC交对称轴于点P,连接PA.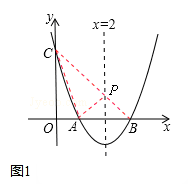
由(1)抛物线解析式为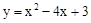 ,A(1,0),B(3,0),
,A(1,0),B(3,0),
∴C(0,3)。
∴ 。
。
∵点A、B关于对称轴x=2对称,∴PA=PB。∴PA+PC=PB+PC。此时,PB+PC=BC。
∴点P在对称轴上运动时,(PA+PB)的最小值等于BC。
∴△APC的周长的最小值=AC+AP+PC=AC+BC=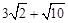 。
。
(3)(2,﹣1)。
解析试题分析:(1)根据抛物线对称轴的定义易求A(1,0),B(3,0),所以设抛物线的顶点式 ,将点A的坐标代入即可求得h,得到抛物线的函数表达式。
,将点A的坐标代入即可求得h,得到抛物线的函数表达式。
(2)如图1,连接AC、BC,BC交对称轴于点P,连接PA.根据抛物线的对称性质得到PA=PB,则△APC的周长的最小值=AC+AP+PC=AC+BC,所以根据两点间的距离公式来求该三角形的周长的最小值即可。
(3)如图2,根据“菱形ADBE的对角线互相垂直平分,抛物线的对称性”得到点D是抛物线 的顶点坐标,即(2,﹣1)。
的顶点坐标,即(2,﹣1)。 

练习册系列答案
相关题目
 .
. ?
? (a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
(a≠0)交x轴于A、B两点,A点坐标为(3,0),与y轴交于点C(0,4),以OC、OA为边作矩形OADC交抛物线于点G.
 (n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线
(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线 与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
 (元)与销售单价
(元)与销售单价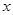 (元)之间的函数关系式;
(元)之间的函数关系式; 的图象经过点A,B,与x轴分别交于点E,F,且点E的坐标为(
的图象经过点A,B,与x轴分别交于点E,F,且点E的坐标为(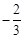 ,0),以OC为直径作半圆,圆心为D.
,0),以OC为直径作半圆,圆心为D.
 .
.