��Ŀ����
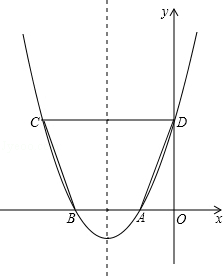
��ͼ����ƽ��ֱ������ϵ�У��ı���OABC�DZ߳�Ϊ2�������Σ����κ��� ��ͼ����A��B����x��ֱ��ڵ�E��F���ҵ�E������Ϊ��
��ͼ����A��B����x��ֱ��ڵ�E��F���ҵ�E������Ϊ��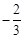 ��0������OCΪֱ������Բ��Բ��ΪD��
��0������OCΪֱ������Բ��Բ��ΪD��
��1������κ����Ľ���ʽ��
��2����֤��ֱ��BE�ǡ�D�����ߣ�
��3����ֱ��BE�������ߵĶԳ��ύ��ΪP��M���߶�CB�ϵ�һ�����㣨��M���B��C���غϣ�������M��MN��BE��x�����N������PM��PN����CM�ij�Ϊt����PMN�����ΪS����S��t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ��S�Ƿ���������ֵ�������ڣ�������ֵ���������ڣ���˵�����ɣ�
�⣺��1�����ı���OABC�DZ߳�Ϊ2�������Σ���A��0��2����B��2��2����
�֡�E������Ϊ��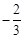 ��0����
��0����
��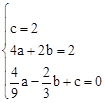 ����ã�
����ã�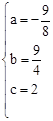 ��
��
��ö��κ����Ľ���ʽΪ��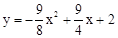 ��
��
��2����ͼ������D��DG��BE�ڵ�G��
�����⣬��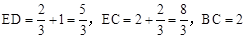 ��
��
��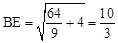 ��
��
�ߡ�BEC=��DEG����EGD=��ECB=90�㣬
���EGD�ס�ECB��
��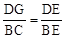 ����
����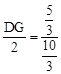 ����DG=1��
����DG=1��
�ߡ�D�İ뾶��1����DG��BE����BE�ǡ�D�����ߡ�
��3�������⣬��E��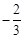 ��0����B��2��2����
��0����B��2��2����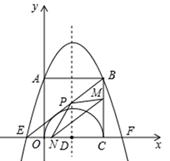
��ֱ��BEΪy=kx+h����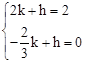 ����ã�
����ã�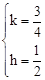 ��
��
��ֱ��BEΪ��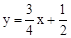 ��
��
��ֱ��BE�������ߵĶԳ��ύ��ΪP���Գ���ֱ��Ϊx=1��
���P��������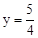 ����P��1��
����P��1��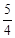 ����
����
��MN��BE�����MNC=��BEC��
�ߡ�C=��C=90�㣬���MNC�ס�BEC����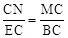 ����
����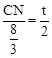 ����
����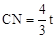 ��
��
��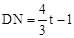 ��
��
�� ��
��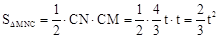 ��
��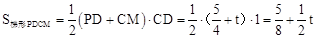 ��
��
��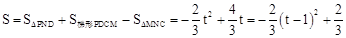 ��0��t��2����
��0��t��2����
��������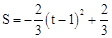 ��0��t��2���Ŀ��ڷ������£�
��0��t��2���Ŀ��ڷ������£�
��S�������ֵ����t=1ʱ��S���=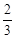 ��
��
����

 ��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д�
��ְٷְټ�����Ԫ��ĩ���Ծ�ϵ�д� Сѧ��ĩ���Ծ�ϵ�д�
Сѧ��ĩ���Ծ�ϵ�д�
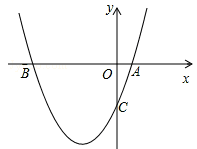
 ��x�ύ�ڵ�A��B��AB=2����y�ύ�ڵ�C���Գ���Ϊֱ��x=2��
��x�ύ�ڵ�A��B��AB=2����y�ύ�ڵ�C���Գ���Ϊֱ��x=2��
 ������A��x���������ϵĵ�B��AO=OB=2����AOB=1200��
������A��x���������ϵĵ�B��AO=OB=2����AOB=1200��

 ��������
��������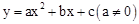 ��x���ཻ��A��B���㣬����A�������Ϊ����3��0����
��x���ཻ��A��B���㣬����A�������Ϊ����3��0����
 ��CΪ��������y��Ľ��㡣
��CΪ��������y��Ľ��㡣 �����P�����ꣻ
�����P�����ꣻ