题目内容
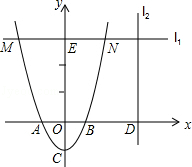
(2013年四川自贡14分)如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA= .
.
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;
(3)在(2)中四边形BMCA面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.
解:(1)如答图1,过点D作DE⊥x轴于点E,则DE=3,OE=2。
∵ ,∴BE=6。
,∴BE=6。
∴OB=BE﹣OE=4。∴B(﹣4,0)。
∵点B(﹣4,0)、D(2,3)在抛物线y=ax2+bx﹣2(a≠0)上,
∴ ,解得
,解得 。
。
∴抛物线的解析式为: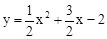 。
。
(2)在抛物线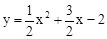 中,
中,
令x=0,得y=﹣2,∴C(0,﹣2)。
令y=0,得x=﹣4或1,∴A(1,0)。
设点M坐标为(m,n)(m<0,n<0)。
如答图1,过点M作MF⊥x轴于点F,则MF=﹣n,OF=﹣m,BF=4+m。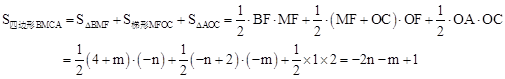
∵点M(m,n)在抛物线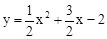 上,∴
上,∴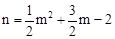 ,代入上式得:
,代入上式得: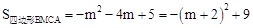 ,
,
∴当m=﹣2时,四边形BMCA面积有最大值,最大值为9。
(3)假设存在这样的⊙Q,
如答图2所示,设直线x=﹣2与x轴交于点G,与直线AC交于点F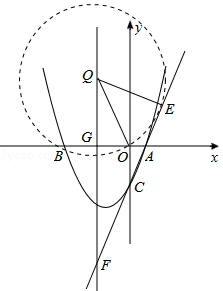
设直线AC的解析式为y=kx+b,
将A(1,0)、C(0,﹣2)代入得: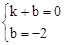 ,解得:
,解得: 。
。
∴直线AC解析式为:y=2x﹣2。
令x=﹣2,得y=﹣6,∴F(﹣2,﹣6),GF=6。
在Rt△AGF中,由勾股定理得: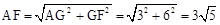 。
。
设Q(﹣2,q),则在Rt△AGF中,由勾股定理得: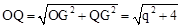 。
。
设⊙Q与直线AC相切于点E,则QE=OQ=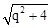 。
。
在Rt△AGF与Rt△QEF中,
∵∠AGF=∠QEF=90°,∠AFG=∠QFE,∴Rt△AGF∽Rt△QEF。
∴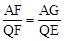 ,即
,即 。
。
化简得: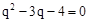 ,解得q=4或q=﹣1。
,解得q=4或q=﹣1。
∴存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆,点Q的坐标为(﹣2,4)或(﹣2,﹣1)。
解析

 与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
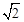 个单位后得到的抛物线的解析式.
个单位后得到的抛物线的解析式.

 上,求此时点F的坐标.
上,求此时点F的坐标.