题目内容
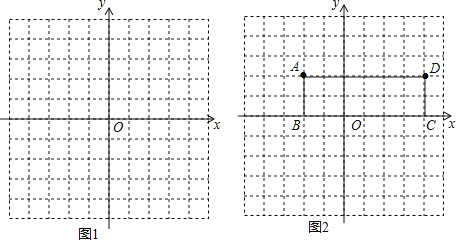
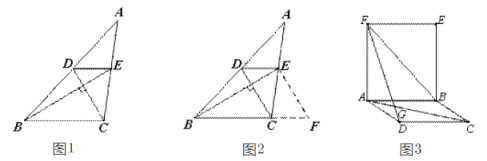
【题目】如图 1,C为线段 AB上一点,以 AC,BC为一边,在 AB同侧做长方形 ACDE和长方形 CBFG,且 满足 AC=2AE,CB=2BF,记 AC2a,BC2b(a b) .
(1)记长方形 ACDE的面积为 s1 ,长方形 CBFG的面积为 s2 .若 AB6, a2b ,求 s1 s2 .
(2)如图 2,点 P是线段 CA上的动点.
①当点 P从点 C向左移动![]() 个单位后,求△EAP与△FBP的面积之差.
个单位后,求△EAP与△FBP的面积之差.
②当点 P从点 C向左移动 ![]() 个单位后,△EAP与△FBP的面积之差记为 m1 ; 当点 P从点 C向左移动 (a b) 个单位后,△EAP与△FBP的面积之差记为 m2 ,求
个单位后,△EAP与△FBP的面积之差记为 m1 ; 当点 P从点 C向左移动 (a b) 个单位后,△EAP与△FBP的面积之差记为 m2 ,求 ![]() 的值(结果用含 n 的代数式表示).
的值(结果用含 n 的代数式表示).
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() n
n![]() .
.
【解析】
(1)根据AC+BC=AB建立方程,求出a,b的值即可解决问题;
(2)①用a,b表示PA,PB的长即可解决问题;
②分别求出m1,m2即可解决问题.
(1)∵AC=2a,BC=2b,a=2b,
∴AC=2BC,
∵AB=6,
∴AC+BC=6,即3BC =6,
∴BC=2,AC=4,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ;
;
(2)①由题意得:![]() ,
,![]() ,
,
∴![]() ;
;
②当点P从点C向左移动![]() (n>1)个单位后,
(n>1)个单位后,
由题意得:![]() ,
,![]() ,
,
∴![]() ,
,
当点P从点C向左移动![]() 个单位后,
个单位后,![]() ,
,![]() ,
,
∴![]() ,
,
∴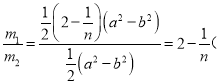 n
n![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目