题目内容
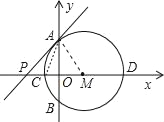
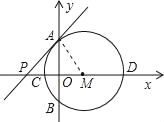
【题目】已知,如图,点M在x轴上,以点M为圆心,2.5长为半径的圆交y轴于A、B两点,交x轴于C(x1,0)、D(x2,0)两点,(x1<x2),x1、x2是方程x(2x+1)=(x+2)2的两根.
(1)求点C、D及点M的坐标;
(2)若直线y=kx+b切⊙M于点A,交x轴于P,求PA的长;
(3)⊙M上是否存在这样的点Q,使点Q、A、C三点构成的三角形与△AOC相似?若存在,请求出点的坐标,并求出过A、C、Q三点的抛物线的解析式;若不存在,请说明理由.

【答案】(1) C(﹣1,0),D(4,0),(1.5,0);(2) ![]() ;(3) 过A、C、Q三点的抛物线的解析式为:y=﹣
;(3) 过A、C、Q三点的抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+2.
x+2.
【解析】解:(1)x(2x+1)=(x+2)2整理得,x2﹣3x﹣4=0,
解得x1=﹣1,x2=4,
∴点C、D的坐标是C(﹣1,0),D(4,0),
![]() =1.5,
=1.5,
∴点M的坐标是(1.5,0),
故答案为:C(﹣1,0),D(4,0),(1.5,0);
(2)如图,连接AM,则AM=2.5,
在Rt△AOM中,AO=![]() =2,
=2,
∴点A的坐标是(0,2),
∵PA与⊙M相切,
∴AM⊥PA,
∴∠MAO+∠PAO=90°,
又∵∠AMO+∠MAO,
∴∠AMO=∠PAO,
在△AOM与△POA中, ![]() ,
,
∴△AOM∽△POA,
∴![]() ,
,
即![]() ,
,
解得PA=![]() ;
;
(3)存在.
如图,连接AC、AD,
∴∠CAD=90°,
在△ACO与△DCA中, ![]() ,
,
∴△ACO∽△DCA,
∴存在点Q,与点D重合时,点Q、A、C三点构成的三角形与△AOC相似,
此时,设过点A、C、Q的抛物线是y=ax2+bx+c,
则 ,
,
解得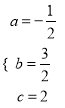 ,
,
∴过A、C、Q三点的抛物线的解析式为:y=﹣![]() x2+
x2+![]() x+2.
x+2.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目