��Ŀ����
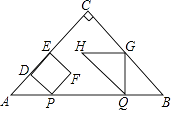
����Ŀ����ͼ1��ƽ��ֱ������ϵ�У�ֱ��AB��x�Ḻ���ύ�ڵ�A��a��0������ y�������ύ�ڵ�B��0��b������![]() +|b��4|=0��
+|b��4|=0��

��1�����AOB�������
��2����ͼ2����PΪֱ��AB��һ���㣬����OP����2S��AOP��S��BOP��3S��AOP����P�������xP��ȡֵ��Χ��
��3����ͼ3����C�ڵ�������ֱ��AB�ϣ�����OC��OE��OC��O������CE��y ���ڵ�D������AD��OE���ӳ�����F�����OAD����ADC����CEF����AOC֮���Ƿ���ij��ȷ����������ϵ����֤����Ľ��ۣ�
���𰸡���1��12����2����4.5��xP�ܩ�4��12��xP�ܩ�9����3����CEF+��ADC����OAD����AOC=90�㣮
��������
��1�����÷Ǹ��������ʼ��ɽ�����⣻
��2������P��PH��y����H����PH=|xP|���������������ۼ��ɢٵ�P�ڵ�һ����ʱ��S��BOP��S��AOP�����۲��������ڵ�P�ڵڶ�����ʱ��PH=|xP|=-xP��S��BOP=-2xP��S��AOP=12+2xP���г�����ʽ���ɽ�����⣮��P�ڵ�������ʱ���г�����ʽ���ɣ�
��3����ͼ����AM��OF��CD��M��DN��OF��OC��N������ƽ���ߵ����ʣ���ʽ�����ʼ��ɽ������.
��1����![]() +|b��4|=0��
+|b��4|=0��
�֡�![]() ��0��|b��4|��0��
��0��|b��4|��0��
��a=��6��b=4��
��A����6��0����B��0��4��
��S��AOB=![]() ��6��4=12��
��6��4=12��
��2����ͼ������P��PH��y����H����PH=|xP|����ͼ�ο�֪��
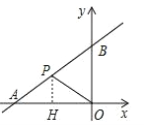
�ٵ�P�ڵ�һ����ʱ��S��BOP��S��AOP�����۲�������
�ڵ�P�ڵڶ�����ʱ��PH=|xP|=��xP��S��BOP=��2xP��S��AOP=12+2xP
��2��12+2xP���ܩ�2xP��3��12+2xP����
��é�4.5��xP�ܩ�4��
��P�ڵ�������ʱ��2����2xP��12���ܩ�2xP��3����2xP��12����
��é�12��xP�ܩ�9��
���ϣ�P�������xP��ȡֵ��Χ�ǩ�4.5��xP�ܩ�4��12��xP�ܩ�9��
��3����ͼ����AM��OF��CD��M��DN��OF��OC��N��
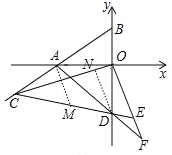
��AM��OF��DN��
���AMD=��CEF����ADN=��DAM����AMD+��ADC+��ADN=180������
��FOC+��AOC+��OAD+��DAM=180�㣬
�֡ߡ�FOC=90�㣬
���OAD+��AOC+��DAM=90������
�ɢٵá�ADN=180�㩁��AMD����ADC���ɢڵá�DAM=90�㩁��OAD����AOC��
�֡�ADN=��DAM��
��180�㩁��AMD����ADC=90�㩁��OAD����AOC��
�֡ߡ�AMD=��CEF��
���CEF+��ADC����OAD����AOC=90�㣮
�����CEF+��ADC=90��+��OAD+��AOC���ƽ��۾��ɣ�

����Ŀ��ʢʢͬѧ��ij��У����ʱ�������˶������������еIJ�����Ϣ�����±�����
Ժϵ�������ɼ����� | |||
�������� | ʤ�� | ���� | ���� |
22 | 12 | 10 | 34 |
22 | 14 | 8 | 36 |
22 | 0 | 22 | 22 |
ʢʢͬѧ���ѧϰ��֪ʶ������������⣬�����æ����������⣺
��1���ӱ��п��Կ�������һ����______��,ʤһ����_______����
��2��ij���ڱ���22����ǰ���£�ʤ���ܻ����ܵ����为���ܻ��ֵ�2������˵������.