��Ŀ����
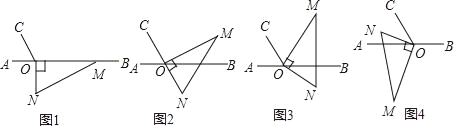
����Ŀ����Rt��ABC�У�BC��AC����ACB��90�㣬DΪ����AB��һ�㣬����CD������C���߶�CD�Ĵ���l����ֱ��l�ϣ��ֱ��ڵ�C�������ȡ���߶�CD��ȵ��߶�CE��CF������AE��BF.
(1)����D���߶�AB��ʱ(��D�����A��B�غ�)����ͼ23(a)��
�����㽫ͼ�β���������
���߶�BF��AD����ֱ�ߵ�λ�ù�ϵΪ________���߶�BF��AD��������ϵΪ________��
(2)����D���߶�AB���ӳ�����ʱ����ͼ23(b)��
��(1)�Т��ʵĽ����Ƿ���Ȼ��������������������֤�����������������˵�����ɣ�

���𰸡�(1)�ټ�����;�ڴ�ֱ�����;(2)����,���ɼ�����.
��������
(1)����ͼ��ʾ��

�ڸ���CD��EF,�ɵá�DCF��90��.���ڡ�ACB��90��,�ɵá�ACB����DCF,��ACD����BCF.
����AC��BC,CD��CF,���ж���ACD�ա�BCF,����ȫ�������ε����ʿɵ�AD��BF,��BAC����FBC,�̶��ɵá�ABF����ABC����FBC����ABC����BAC��90��,��BF��AD.
(2)����CD��EF,�ɵá�DCF��90��,���ڡ�ACB��90��,��֤��DCF����ACB,
���ԡ�DCF����BCD����ACB����BCD,�̶��ɵá�BCF����ACD,����AC��BC,CD��CF,
���ж���ACD�ա�BCF,����ȫ�������ε����ʿɵ�AD��BF,��BAC����FBC,���ԡ�ABF����ABC����FBC����ABC����BAC��90��,��BF��AD.
��:(1)����ͼ��ʾ��

�ڡ�CD��EF,
���DCF��90��.
�ߡ�ACB��90��,
���ACB����DCF,
���ACD����BCF.
�֡�AC��BC,CD��CF,
���ACD�ա�BCF,
��AD��BF,��BAC����FBC,
���ABF����ABC����FBC����ABC����BAC��90��,��BF��AD.
�ʴ�Ϊ:��ֱ,���.
(2)������
֤��:��CD��EF,
���DCF��90��,
�ߡ�ACB��90��,
���DCF����ACB,
���DCF����BCD����ACB����BCD,
���BCF����ACD,
�֡�AC��BC,CD��CF,
���ACD�ա�BCF,
��AD��BF,��BAC����FBC,
���ABF����ABC����FBC����ABC����BAC��90��,��BF��AD.

����Ŀ�����������Խ��Խ�ܵ����ǵ�ϲ����˳�糵�о�Ӫ��A�ͳ�2016��4�·������ܶ�Ϊ3.2��Ԫ�����꾭������������A�ͳ�ÿ�����۱�ȥ������400Ԫ��������4�·���ȥ��4�·�������A�ͳ�������ͬ�������4�·�A�ͳ������ܶ��ȥ��4�·������ܶ�����25%�� A��B�����ͺų��Ľ��������ۼ۸������
A�ͳ� | B�ͳ� | |
�����۸�Ԫ/���� | 1100 | 1400 |
���ۼ۸�Ԫ/���� | ��������ۼ۸� | 2400 |
��1�������4�·�A�ͳ�ÿ�����ۼ۶���Ԫ�����з��̵ķ�����𣩣�
��2���ó��мƻ�5�·��½�һ��A�ͳ���B�ͳ���50������B�ͳ��Ľ�������������A�ͳ�������������Ӧ��ν�������ʹ������������ࣿ