Question

如图，在平面直角坐标系中，点P从原点O出发按图中“→”方向运动，每次运动1个单位长度，得到点P₁、P₂、P₃、P₄、P₅、P₆、…，且△OP₁P₂、△P₂P₄P₆、△P₆P₉P₁₂…都是等边三角形，则P₁的坐标是______，P₄₂₀的坐标是______．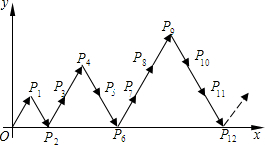

Answer 1

∵△OP₁P₂是等边三角形，
∴∠P₁OP₂=60°，
1×cos60°=1×

1

2

=

1

2

，
1×sin60°=1×

3

2

=

3

2

，
∴点P₁的坐标是（

1

2

，

3

2

）；

∵第1个三角形有2个点，
第2个三角形增加4个点，
第3个三角形增加6个点，
…，
依此规律，第n个三角形增加2n个点，
∴2+4+6+…+2n=

(2+2n)•n

2

，

(2+2n)•n

2

=420，
整理得，n²+n-420=0，
解得n=20，n=-21（舍去），
∴P₄₂₀是第20个三角形最后的一个点，在x轴上，
∵1+2+3+…+20=

(1+20)•20

2

=210，
∴P₄₂₀的坐标是（210，0）．
故答案为：（

1

2

，

3

2

）；（210，0）．