题目内容

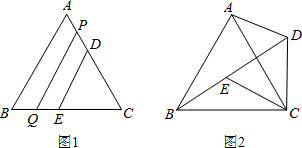
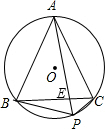
如图，正△ABC内接于⊙O，P是劣弧BC上任意一点，PA与BC交于点E，有如下结论：①PA=PB+PC；②
1
PA
=
1
PB
+
1
PC
；③PA•PE=PB•PC．其中，正确结论的个数为（　　）
A．3个B．2个C．1个D．0个

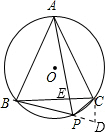
延长BP到D，使PD=PC，连接CD，可得∠CPD=∠BAC=60°，
则△PCD为等边三角形，
∵△ABC为正三角形，
∴BC=AC
∵∠PBC=∠CAP，∠CPA=∠CDB，
∴△APC≌△BDC（AAS）．
∴PA=DB=PB+PD=PB+PC，故①正确；
由（1）知△PBE∽△PAC，则
PA
PC
=
PB
PE
，
PA
PB
=
PC
PE
，
PA
PB
+
PA
PC
=
PC
PE
+
PB
PE
≠1，
∴②错误；
∵∠CAP=∠EBP，∠BPE=∠CPA
∴△PBE∽△PAC
∴
PA
PB
=
PC
PE

∴PA•PE=PB•PC，故③正确；
故选B．
练习册系列答案
相关题目
图①是一块边长为1，周长记为P1的正三角形纸板，沿图①的底边剪去一块边长为
1
2
的正三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的正三角形纸板（即其边长为前一块被剪如图掉正三角形纸板边长的
1
2
）后，得图③，④，…，记第n（n≥3）块纸板的周长为Pn，则Pn-Pn-1的值为（　　）
A．(
1
4
)n-1		B．(
1
4
)n		C．(
1
2
)n-1		D．(
1
2
)n
如图，△ABP与△CDP是两个全等的等边三角形，且PA⊥PD．有下列四个结论：
（1）∠PBC=15°；（2）AD∥BC；（3）直线PC与AB垂直；（4）四边形ABCD是轴对称图形．
其中正确结论个数是（　　）
A．1B．2C．3D．4
如图，将边长为4的等边△ABC，沿x轴向左平移2个单位后，得到△A′B′C′，则点A′的坐标为______．
如图，已知等边△ABC和等边△CDE，P、Q分别为AD、BE的中点．
（1）试判断△CPQ的形状并说明理由．
（2）如果将等边△CDE绕点C旋转，在旋转过程中△CPQ的形状会改变吗？请你将图2中的图形补画完整并说明理由．
下面四个说法：
①有两个角是60°的三角形是等边三角形；
②三个不同的外角都相等的三角形是等边三角形；
③每边上的高也是这边上的中线的三角形是等边三角形；
④内角是60°的外角平分线平行于这个内角的对边的三角形是等边三角形．
其中正确的个数是（　　）
A．4个B．3个C．2个D．1个
如图，在平面直角坐标系中，点P从原点O出发按图中“→”方向运动，每次运动1个单位长度，得到点P1、P2、P3、P4、P5、P6、…，且△OP1P2、△P2P4P6、△P6P9P12…都是等边三角形，则P1的坐标是______，P420的坐标是______．
已知如下图所示，在等边△ABC和等边△ADE中，点B、A、D在一条直线上，BE、CD交于F．
（1）求证：△BAE≌△CAD．
（2）求∠BFC的大小．
（3）在图1的基础上，将△ADE绕点A按顺时针方向旋转180°，此时BE交CD的延长线于点F，其他条件不变，得到图2所示的图形，请直接写出（1）、（2）中结论是否仍然成立．
以边长为2厘米的正三角形的高为边长作第二个正三角形，以第二个正三角形的高为边长作第三个正三角形，以此类推，则第十个正三角形的边长是（　　）
A．2×（
2
2
）10厘米		B．2×（
1
2
）9厘米		C．2×（
3
2
）10厘米		D．2×（
3
2
）9厘米

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网