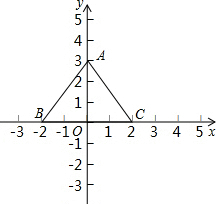题目内容
已知：如图，边长为2的等边三角形ABC，延长BC到D，使CD=BC，延长CB到E，使BE=CB，求△ADE的周长．
证明：∵△ABC是等边三角形，边长为2，
∴∠ABC=∠ACB=60°，AB=CB=AC=2，
∴∠E+∠EAB=∠ABC=60°，
∵BE=CB，
∴AB=BE，EC=EB+BC=4，
∴∠E=∠EAB=30°，
∴∠EAC=90°，
∴AE=
=2
，
同理可得：AD=2
，
∵DE=3BC=6，
∴△ADE的周长是6+2
+2
=6+4
．
∴∠ABC=∠ACB=60°，AB=CB=AC=2，
∴∠E+∠EAB=∠ABC=60°，
∵BE=CB，
∴AB=BE，EC=EB+BC=4，
∴∠E=∠EAB=30°，
∴∠EAC=90°，
∴AE=
| 42-22 |
| 3 |
同理可得：AD=2
| 3 |
∵DE=3BC=6，
∴△ADE的周长是6+2
| 3 |
| 3 |
| 3 |
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
