题目内容
如图，已知△ABC是等边三角形，E是AC延长线上一点，选择一点D，使得△CDE是等边三角形，如果M是线段AD的中点，N是线段BE的中点，
求证：△CMN是等边三角形．
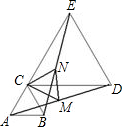
求证：△CMN是等边三角形．
证明：∵△ABC是等边三角形，△CDE是等边三角形，M是线段AD的中点，N是线段BE的中点，
∴∠ACB=∠ECD=60°，
∴∠ACB+∠BCD=∠ECD+∠BCD，即∠ACD=∠BCE，
在△ACD和△BCE中，
，
∴△ACD≌△BCE，
∴AD=BE，AM=BN；
∴AC=BC，∠CAD=∠CBE，AM=BN，
∴△AMC≌△BNC（SAS），
∴CM=CN，∠ACM=∠BCN；
又∵∠NCM=∠BCN-∠BCM，
∠ACB=∠ACM-∠BCM，
∴∠NCM=∠ACB=60°，
∴△CMN是等边三角形．
M是线段AD的中点，N是线段BE的中点，∴∠ACB=∠ECD=60°，
∴∠ACB+∠BCD=∠ECD+∠BCD，即∠ACD=∠BCE，
在△ACD和△BCE中，
|
∴△ACD≌△BCE，
∴AD=BE，AM=BN；
∴AC=BC，∠CAD=∠CBE，AM=BN，
∴△AMC≌△BNC（SAS），
∴CM=CN，∠ACM=∠BCN；
又∵∠NCM=∠BCN-∠BCM，
∠ACB=∠ACM-∠BCM，
∴∠NCM=∠ACB=60°，
∴△CMN是等边三角形．
练习册系列答案
相关题目
