题目内容
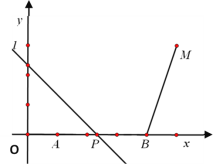
【题目】如图,圆O的半径为3cm,B为圆O外一点,OB交圆O于A,AB=OA,动点P从点A出发,以πcm/s的速度在圆O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为( )秒时,BP与圆O相切.
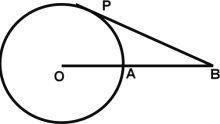
A.1sB.5sC.1s或 5sD.2s或 4s
【答案】C
【解析】
根据切线的判定与性质进行分析即可.若BP与⊙O相切,则∠OPB=90°,又因为OB=2OP,可得∠B=30°,则∠BOP=60°;根据弧长公式求得弧AP长,除以速度,即可求得时间.
解:连接OP;
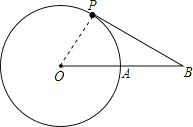
∵当OP⊥PB时,BP与⊙O相切,
∵AB=OA,OA=OP,
∴OB=2OP,∠OPB=90°;
∴∠B=30°;
∴∠O=60°;
∵OA=3cm,
弧AP=![]() ,
,
∵圆的周长为:6π,
∴点P运动的距离为π或6π-π=5π;
∴当t=1或5时,有BP与⊙O相切.
故选:C.

【题目】中考将近,同学们需要花更多的时间来进行自我反思和总结,消化白天的学习内容,提高学习效率.因此,每个班都在积极地进行自我调整.我校A班和B班的同学也积极响应号召,调查了本班的自习情况以供老师参考.
A班同学在班级抽样调查中,调查了十名同学的学习情况,将这十名同学在一周内每天用于自主复习的总时间四舍五入后,分别记录如下:(单位:分)
18 11 22 25 25 18 27 25 22 27
B班的同学采取的普查方式,让每位同学自己写出平均每天的自主复习时间,将数据收集整理后得到以下数据:
平均数 | 中位数 | 众数 | 极差 | 方差 |
22 | 23 | 30 | 30 | 59.7 |
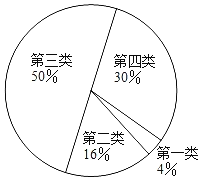
B班的同学还将自主复习时间分为四大类:第一类为时间小于10分钟以下;第二类为时间大于或等于10分钟且小于20分钟;第三类为时间大于或等于20分钟且小于30分钟;第四类为时间大于或等于30分钟,并得到如下的扇形图.
(1)在扇形图中,第一类所对的圆心角度数为 .
(2)写出A班被调查同学的以下特征数.
平均数 | 中位数 | 众数 | 极差 | 方差 |
22 | 25 | 16 |
(3)从上面的数据,我们可以得到 班的自主复习情况要好一些.其理由为(至少两条): .