题目内容
【题目】如图,在平行四边形ABCD中,点E,F分别是AB,CD的中点.

(1)求证:四边形AEFD是平行四边形;(2)若∠A=60°,AB=2AD=4,求BD的长.
【答案】(1)证明见解析;(2) BD=![]() .
.
【解析】
(1)利用一组对边平行且相等的四边形是平行四边形,证明四边形AEFD是平行四边形;
(2)过点D作DG⊥AB于点G,利用已知条件和锐角三角函数以及勾股定理即可求出BD的长..
(1)∵四边形ABCD是平行四边形,
∴AB‖CD且AB=CD
∵E,F分别是AB,CD的中点,
∴![]()
∴AE=DF
∴四边形AEFD是平行四边形;
(2)过点D作DG⊥AB于点G.
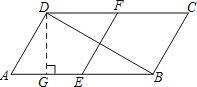
∵AB=2AD=4,
∴AD=2.
在Rt△AGD中,∵∠AGD=90°,∠A=60°,AD=2,
∴![]() ,
,![]() ,
,
∴BG=AB-AG=3
在Rt△DGB中,∵∠DGB=90°,DG=![]() ,BG=3,
,BG=3,
∴![]()

练习册系列答案
相关题目