题目内容
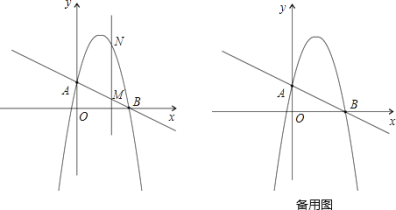
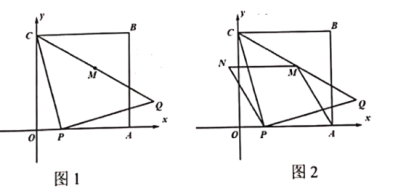
【题目】如图,点A(1, 0)、B(4,0)、M(5,3).动点P从A点出发,沿x轴以每秒1个单位的速度向右移动,过点P的直线l:y= -x+b也随之移动.设移动时间为t秒.
(1)当t=1时,求直线l的解析式.
(2)若直线l与线段BM有公共点,求t的取值范围.
(3)当点M关于直线l的对称点落在坐标轴上时,求t的值.
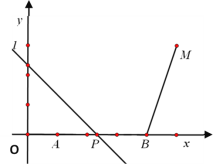
【答案】(1)y=-x+2;(2)3≤t≤7;(3)t=2或4
【解析】
(1)先根据点P的运动路径表示出点P的坐标,然后将t=1代入即可得出点P的坐标,最后根据待定系数法即可确定l的解析式;
(2)先分别找出直线l过点B、M时b的值,然后再根据一次函数图像上点的坐标特征解答即可;
(3)分对称点落在x轴和y轴上两种情况讨论,先用待定系数法求出直线MC的解析式,则直线MC与x、y轴的交点将是点M关于直线l的对称点,再找出两直线的交点坐标,最后根据一次函数图像上的点坐标特征解答即可.
解:(1)直线y=-x+b交x轴于点P(1+t,0)
由题意,得b>0,t≥0
当t=1时,-2+b=0
解得b=2
故y=-x+2;
(2)当直线y=-x+b过点B(4,0)时,0=-4+b,得:b=4,0=-(1+t)+4,解得t=3.
当直线y=-x+b过点M(5,3)时,3=-5+b,得:b=8,0=-(1+t)+8,解得t=7.
故若l与线段BM有公共点,t的取值范围是:3≤t≤7.
(3)如图,过点M作MC⊥直线l,交y轴于点C,交直线l于点D,则点C为点M在坐标轴上的对称点.设直线MC的解析式为y=x+m,则:3=5+m,解得m=-2,
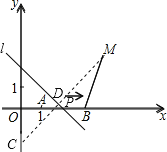
故直线MC的解析式为y=x-2.
当x=0时,y=0-2=-2,则C点坐标为(0,-2),
∵(0+5)÷2=2.5,(3-2)÷2=0.5,∴D点坐标为(2.5,0.5),
当直线y=-x+b过点D(2.5,0.5)时,0.5=-2.5+b,解得:b=3,
0=-(1+t)+3,解得t=2.∴t为2时,点M关于l的对称点落在y轴上.
直线MC分别与x轴、直线l交与点E,F,则E(2, 0)
F(3.5, 1.5 ).即1.5=-3.5+b, b=5
t=4时点M关于l的对称点落在x轴上
综上,t=2或4时,M的对称点在坐标轴上.

 名校课堂系列答案
名校课堂系列答案