题目内容
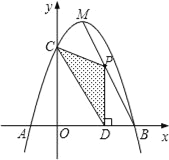
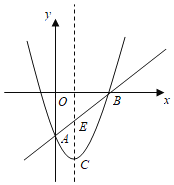
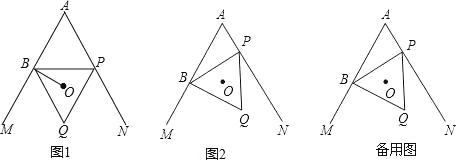
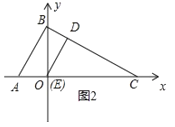
【题目】如图 1,直线 y=2x+2 分别交 x 轴、y 轴于点A、B,点C为x轴正半轴上的点,点 D从点C处出发,沿线段CB匀速运动至点 B 处停止,过点D作DE⊥BC,交x轴于点E,点 C′是点C关于直线DE的对称点,连接 EC′,若△ DEC′与△ BOC 的重叠部分面积为S,点D的运动时间为t(秒),S与 t 的函数图象如图 2 所示.
(1)VD ,C 坐标为 ;
(2)图2中,m= ,n= ,k= .
(3)求出S与t 之间的函数关系式(不必写自变量t的取值范围).
【答案】(1)点D的运动速度为1单位长度/秒,点C坐标为(4,0).(2)![]() ;
;![]() ;
;![]() .(3)①当点C′在线段BC上时, S=
.(3)①当点C′在线段BC上时, S=![]() t2;②当点C′在CB的延长线上, S=
t2;②当点C′在CB的延长线上, S=![]() t2+
t2+![]() t
t![]() ;③当点E在x轴负半轴, S=t24
;③当点E在x轴负半轴, S=t24![]() t+20.
t+20.
【解析】
(1)根据直线的解析式先找出点B的坐标,结合图象可知当t=![]() 时,点C′与点B重合,通过三角形的面积公式可求出CE的长度,结合勾股定理可得出OE的长度,由OC=OE+EC可得出OC的长度,即得出C点的坐标,再由勾股定理得出BC的长度,根据CD=
时,点C′与点B重合,通过三角形的面积公式可求出CE的长度,结合勾股定理可得出OE的长度,由OC=OE+EC可得出OC的长度,即得出C点的坐标,再由勾股定理得出BC的长度,根据CD=![]() BC,结合速度=路程÷时间即可得出结论;
BC,结合速度=路程÷时间即可得出结论;
(2)结合D点的运动以及面积S关于时间t的函数图象的拐点,即可得知当“当t=k时,点D与点B重合,当t=m时,点E和点O重合”,结合∠C的正余弦值通过解直角三角形即可得出m、k的值,再由三角形的面积公式即可得出n的值;
(3)随着D点的运动,按△DEC′与△BOC的重叠部分形状分三种情况考虑:①通过解直角三角形以及三角形的面积公式即可得出此种情况下S关于t的函数关系式;②由重合部分的面积=S△CDES△BC′F,通过解直角三角形得出两个三角形的各边长,结合三角形的面积公式即可得出结论;③通过边与边的关系以及解直角三角形找出BD和DF的值,结合三角形的面积公式即可得出结论.
(1)令x=0,则y=2,即点B坐标为(0,2),
∴OB=2.
当t=![]() 时,B和C′点重合,如图1所示,
时,B和C′点重合,如图1所示,
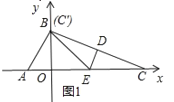
此时S=![]() ×
×![]() CEOB=
CEOB=![]() ,
,
∴CE=![]() ,
,
∴BE=![]() .
.
∵OB=2,
OE=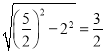 ,
,
∴OC=OE+EC=![]() +
+![]() =4,BC=
=4,BC=![]() ,CD=
,CD=![]() ,
,
![]() ÷
÷![]() =1(单位长度/秒),
=1(单位长度/秒),
∴点D的运动速度为1单位长度/秒,点C坐标为(4,0).
故答案为:1单位长度/秒;(4,0);
(2)根据图象可知:
当t=k时,点D与点B重合,
此时k=![]() =2
=2![]() ;
;
当t=m时,点E和点O重合,如图2所示.
sin∠C=![]() =
=![]() =
=![]() ,cos∠C=
,cos∠C=![]() ,
,
OD=OCsin∠C=4×![]() =
=![]() ,CD=OCcos∠C=4×
,CD=OCcos∠C=4×![]() =
=![]() .
.
∴m=![]() =
=![]() ,n=
,n=![]() BDOD=
BDOD=![]() ×(2
×(2![]()
![]() )×
)×![]() =
=![]() .
.
故答案为:![]() ;
;![]() ;2
;2![]() .
.
(3)随着D点的运动,按△DEC′与△BOC的重叠部分形状分三种情况考虑:
①当点C′在线段BC上时,如图3所示.
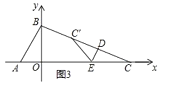
此时CD=t,CC′=2t,0<CC′≤BC,
∴0<t≤![]() .
.
∵tan∠C=![]() ,
,
∴DE=CDtan∠C=![]() t,
t,
此时S=![]() CDDE=
CDDE=![]() t2;
t2;
②当点C′在CB的延长线上,点E在线段OC上时,如图4所示.

此时CD=t,BC′=2t2![]() ,DE=CDtan∠C=
,DE=CDtan∠C=![]() t,CE=
t,CE=![]() =
=![]() t,OE=OCCE=4
t,OE=OCCE=4![]() t,
t,
∵![]() ,即
,即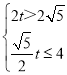 ,
,
解得:![]() <t≤
<t≤![]() .
.
由(1)可知tan∠OEF=![]() =
=![]() ,
,
∴OF=OEtan∠OEF=![]() t,BF=OBOF=
t,BF=OBOF=![]() ,
,
∴FM=BFcos∠C=![]() .
.
此时S=![]() CDDE
CDDE![]() BC′FM=
BC′FM=![]() ;
;
③当点E在x轴负半轴,点D在线段BC上时,如图5所示.
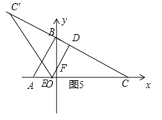
此时CD=t,BD=BCCD=2![]() t,CE=
t,CE=![]() t,DF=
t,DF=![]() ,
,
∵![]() ,即
,即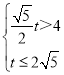 ,
,
∴![]() <t≤2
<t≤2![]() .
.
此时S=![]() BDDF=
BDDF=![]() ×2×(2
×2×(2![]() t)2=t24
t)2=t24![]() t+20.
t+20.
综上,当点C′在线段BC上时, S=![]() t2;当点C′在CB的延长线上, S=
t2;当点C′在CB的延长线上, S=![]() t2+
t2+![]() t
t![]() ;当点E在x轴负半轴, S=t24
;当点E在x轴负半轴, S=t24![]() t+20.
t+20.

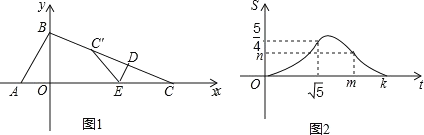
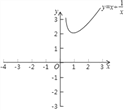
【题目】某数学兴趣小组对函数y=x+![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
x | … | ﹣3 | ﹣2 | ﹣1 | - | - |
|
| 1 | 2 | 3 | … |
y | … | - | m | ﹣2 | - | - |
|
| 2 |
|
| … |
(1)自变量x的取值范围是 ,m= .
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现:
①方程x+![]() =3有 个实数根;
=3有 个实数根;
②若关于x的方程x+![]() =t有2个实数根,则t的取值范围是 .
=t有2个实数根,则t的取值范围是 .
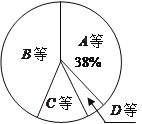
【题目】某校为了解九年级男生1000米长跑的成绩,从中随机抽取了50名男生进行测试,根据测试评分标准,将他们的得分进行统计后分为A、B、C、D四等,并绘制成下面的频数分布表和扇形统计图.
等第 | 成绩(得分) | 频数(人数) | 频率 |
A | 10分 | 7 | 0.14 |
9分 | x | m | |
B | 8分 | 15 | 0.30 |
7分 | 8 | 0.16 | |
C | 6分 | 4 | 0.08 |
5分 | y | n | |
D | 5分以下 | 3 | 0.06 |
合计 | 50 | 1.00 |
(1)试直接写出
(2)求表示得分为C等的扇形的圆心角的度数;
(3)如果该校九年级共有男生200名,试估计这200名男生中成绩达到A等和B等的人数共有多少人?