题目内容
【题目】中考将近,同学们需要花更多的时间来进行自我反思和总结,消化白天的学习内容,提高学习效率.因此,每个班都在积极地进行自我调整.我校A班和B班的同学也积极响应号召,调查了本班的自习情况以供老师参考.
A班同学在班级抽样调查中,调查了十名同学的学习情况,将这十名同学在一周内每天用于自主复习的总时间四舍五入后,分别记录如下:(单位:分)
18 11 22 25 25 18 27 25 22 27
B班的同学采取的普查方式,让每位同学自己写出平均每天的自主复习时间,将数据收集整理后得到以下数据:
平均数 | 中位数 | 众数 | 极差 | 方差 |
22 | 23 | 30 | 30 | 59.7 |
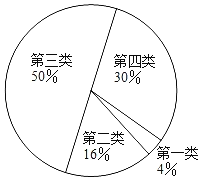
B班的同学还将自主复习时间分为四大类:第一类为时间小于10分钟以下;第二类为时间大于或等于10分钟且小于20分钟;第三类为时间大于或等于20分钟且小于30分钟;第四类为时间大于或等于30分钟,并得到如下的扇形图.
(1)在扇形图中,第一类所对的圆心角度数为 .
(2)写出A班被调查同学的以下特征数.
平均数 | 中位数 | 众数 | 极差 | 方差 |
22 | 25 | 16 |
(3)从上面的数据,我们可以得到 班的自主复习情况要好一些.其理由为(至少两条): .
【答案】(1)14.4°;(2)23.5,25.25;(3)①A班的中位数、众数都比B班的要高一些;②A班的极差、方差都比B班的要小一些,比B班的稳定.
【解析】
(1)第一类占4%,因此圆心角的度数就占360°的4%,求360°×4%即可;(2)将A班的成绩排序后中间两个数的平均数即为中位数,利用方差公式计算方差,填入表格,(3)从中位数、众数、极差、方差等方面选择说明即可.
解:(1)360°×4%=14.4°
故答案为:14.4°,
(2)A组的中位数:(22+25)÷2=23.5,
方差:S2=![]() [(11﹣23.5)2+(18﹣23.5)2×2+(22﹣23.5)2×2+(25﹣23.5)2×3+(27﹣23.5)2×2]=25.25,
[(11﹣23.5)2+(18﹣23.5)2×2+(22﹣23.5)2×2+(25﹣23.5)2×3+(27﹣23.5)2×2]=25.25,
填表如下:

(3)从上面的数据,我们可以得到A班的自主复习情况要好一些;其理由为:①A班的中位数、众数都比B班的要高一些;②A班的极差、方差都比B班的要小一些,比B班的稳定.

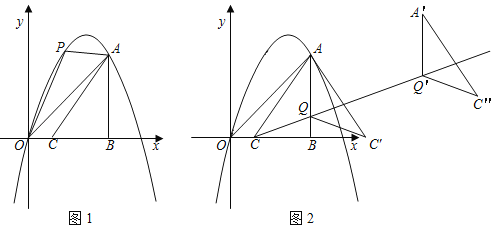
【题目】某数学兴趣小组对函数y=x+![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
x | … | ﹣3 | ﹣2 | ﹣1 | - | - |
|
| 1 | 2 | 3 | … |
y | … | - | m | ﹣2 | - | - |
|
| 2 |
|
| … |
(1)自变量x的取值范围是 ,m= .
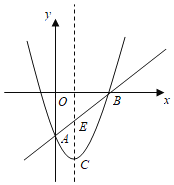
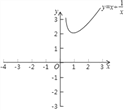
(2)根据(1)中表内的数据,在如图所示的平面直角坐标系中描点,画出函数图象的一部分,请你画出该函数图象的另一部分.
(3)请你根据函数图象,写出两条该函数的性质;
(4)进一步探究该函数的图象发现:
①方程x+![]() =3有 个实数根;
=3有 个实数根;
②若关于x的方程x+![]() =t有2个实数根,则t的取值范围是 .
=t有2个实数根,则t的取值范围是 .
【题目】由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表:
| 甲 | 乙 |
原料成本 | 12 | 8 |
销售单价 | 18 | 12 |
生产提成 | 1 | 0.8 |
(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入﹣投入总成本)