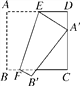
题目内容
【题目】如图,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上.点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,1cm半径作⊙O.点P与点D同时出发,设它们的运动时间为t(单位:s) (0≤t≤![]() ).
).
(1)如图1,连接DQ,若DQ平分∠BDC,则t的值为 s;
(2)如图2,连接CM,设△CMQ的面积为S,求S关于t的函数关系式;
(3)在运动过程中,当t为何值时,⊙O与MN第一次相切?
【答案】(1)1s; (2)S=﹣![]() t2+
t2+![]() t;(3)
t;(3)![]() .
.
【解析】试题分析:(1)由△DQC≌△DQP,推出DP=DC=6,在Rt△ADB中,BD=10,推出PB=4即可解决问题;
(2)过点M作MH⊥BC于点H,证明△HMQ∽△PQB,,由![]() =
=![]() ,得MH=
,得MH=![]() t,即可求得△CMQ的面积;
t,即可求得△CMQ的面积;
(3)设⊙O与MN相切于点E,连接OE,作OF⊥BD于点F,可证得△DFO∽△DCB,
由此![]() 即可解得:t值.
即可解得:t值.
试题解析:(1)∵四边形ABCD为矩形,
∴AB=CD=6cm、AD=BC=8cm,
则DB=10cm,
∵四边形PQMN为正方形,
∴∠BPQ=∠C=90°,
∵∠PBQ=∠CBD,
∴△BPQ∽△BCD,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
则BQ=5t、PQ=3t,
∴CQ=BC﹣BQ=8﹣5t,
∵DQ平分∠BDC,
∴QP=QC,即3t=8﹣5t,
解得:t=1,
故答案为:1;
(2)如图a,过点M作MH⊥BC于点H,
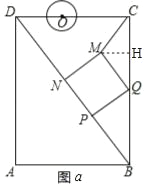
∴∠MHQ=∠QPB=∠MQP=90°,
则∠HMQ+∠HQM=∠PQB+∠HQM=90°,
∴∠HMQ=∠PQB,
∴△HMQ∽△PQB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
则MH=![]() t,
t,
∴S=![]() ×(8﹣5t)
×(8﹣5t)![]() t=﹣
t=﹣![]() t2+
t2+![]() t;
t;
(3)如图b,设⊙O与MN相切于点E,连接OE,作OF⊥BD于点F,
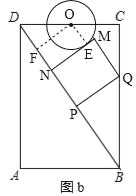
则四边形OENF为矩形,
∴OE=FN=1,∠DFO=∠C=90°,
∵∠FDO=∠CDB,
∴△DFO∽△DCB,
∴![]() ,即
,即![]() ,
,
解得:t=![]() .
.

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案【题目】某文具店准备购进A、B两种型号的书包共50个进行销售,两种书包的进价、售价如下表所示:
书包型号 | 进价(元/个) | 售价(元/个) |
A型 | 200 | 300 |
B型 | 100 | 150 |
购进这50个书包的总费用不超过7300元,且购进B型书包的个数不大于A型书包个数的![]() .
.
(1)该文具店有哪几种进货方案?
(2)若该文具店购进的50个书包全部售完,则该文具店采用哪种进货方案,才能获得最大利润?最大利润是多少?(利润=售价﹣进价)