题目内容
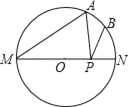
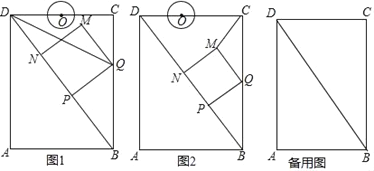
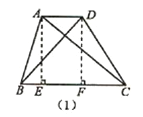
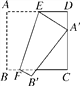
【题目】如图,正方形纸片ABCD的边长为12,E,F分别是边AD,BC上的点,将正方形纸片沿EF折叠,使得点A落在CD边上的点A′处,此时点B落在点B′处.已知折痕EF=13,则AE的长等于_________.
【答案】![]()
【解析】过点F作FG⊥AD,垂足为G,连接AA′,在△GEF中,由勾股定理可求得EG=5,轴对称的性质可知AA′⊥EF,由同角的余角相等可证明∠EAH=∠GFE,从而可证明△ADA′≌△FGE,故此可知GE=DA′=5,最后在△EDA′利用勾股定理列方程求解即可.
解:过点F作FG⊥AD,垂足为G,连接AA′.
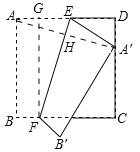
在Rt△EFG中,EG=![]() ,
,
∵轴对称的性质可知AA′⊥EF,
∴∠EAH+∠AEH=90.
∵FG⊥AD,
∴∠GEF+∠EFG=90.
∴∠DAA′=∠GFE.
在△GEF和△DA′A中,
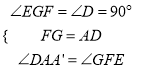 ,
,
∴△GEF≌△DA′A.
∴DA′=EG=5.
设AE=x,由翻折的性质可知EA′=x,则DE=12x.
在Rt△EDA′中,由勾股定理得:A′E2=DE2+A′D2,即x2=(12x)2+52.
解得:x=![]() .
.
故答案为: ![]() .
.

练习册系列答案
相关题目