题目内容
【题目】数学活动——探究特殊的平行四边形.
问题情境
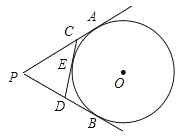
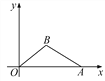
如图,在四边形ABCD中,AC为对角线,AB=AD,BC=DC.请你添加条件,使它们成为特殊的平行四边形.

提出问题
(1)第一小组添加的条件是“AB∥CD”,则四边形ABCD是菱形.请你证明;
(2)第二小组添加的条件是“∠B=90°,∠BCD=90°”,则四边形ABCD是正方形.请你证明.
【答案】(1)见解析证明;(2)见解析证明.
【解析】
试题分析:(1)根据SSS可判定△ABC≌△ADC,根据全等三角形对应角相等和两直线平行内错角相等可得∠BAC=∠DCA=∠BCA=∠DAC,根据等角对等边可得AB=BC=CD=DA,即得结论;(2)由△ABC≌△ADC得∠D =∠B=90°,又∠BCD=90°,可判定四边形BCD是矩形,又因BC=DC,即可得出结论.
试题解析:(1)∵AB=AD,BC=DC,AC=AC,∴△ABC≌△ADC,∴∠BAC=∠DAC,∠BCA=∠DCA,又∵AB∥CD,∴∠BAC=∠DCA,∴∠BAC=∠DCA=∠BCA=∠DAC,∴AB=BC,DA=DC,又∵AB=AD,∴AB=BC=CD=DA,∴四边形ABCD是菱形;
(2)∵AB=AD,BC=DC,AC=AC,∴△ABC≌△ADC,∴∠D =∠B,∵∠B=90°,∴∠D =∠B=90°,又∵∠BCD=90°,∴四边形ABCD是矩形,又∵BC=DC,∴矩形ABCD是正方形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某种蔬菜的价格随季节变化如下表,根据表中信息,下列结论错误的是( )
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
价格 | 5.00 | 5.50 | 5.00 | 4.80 | 2.00 | 1.50 | 1.00 | 0.90 | 1.50 | 3.00 | 2.50 | 3.50 |
A. ![]() 是自变量,
是自变量,![]() 是因变量
是因变量
B. 2月份这种蔬菜价格最高,为5.50元/千克
C. 2-8月份这种蔬菜价格一直在下降
D. 8-12月份这种蔬菜价格一直在上升