题目内容
【题目】如图,在等边三角形ABC中,AB=4.作BM平分∠ABC交AC于点M,点D为射线BM上一点,以点B为旋转中心将线段BD逆时针旋转60°得到线段BE,连接DE.交射线BA于点F,连接AD、AE.当以A、D、M为顶点的三角形与△AEF全等时,DE的长为______.
【答案】![]() ,4,
,4,![]()
【解析】
分点D在线段BM上,点D在线段BM的延长线上时,两种情形分别求解即可.
解:如图,
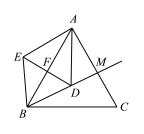
当△AFE≌△AMD时,AF=AM,
∵∠AFD=∠AMD=90°,
∵AD=AD,
∴Rt△ADF≌Rt△ADM(HL),
∴∠DAF=∠DAM=30°,
∴∠DBA=∠DAB=30°,
∴DA=DB,
∵DF⊥AB,
∴∠BDF=60°,BF=AF=2,
∵BD=BE,
∴△BDE是等边三角形,
∴DF=EF=BFtan30°=![]() ,
,
∴DE=2EF=![]() .
.
如图,当点D在BM的延长线时,易证AF=AM=2,DE=2DF=![]() .
.
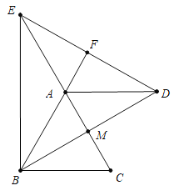
如图,当EF=AM=DF时,也满足条件,此时DE=BD=AB=4,
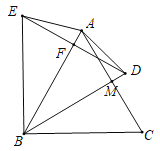
故答案为:![]() 或
或![]() 或4.
或4.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
【题目】某种蔬菜的价格随季节变化如下表,根据表中信息,下列结论错误的是( )
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
价格 | 5.00 | 5.50 | 5.00 | 4.80 | 2.00 | 1.50 | 1.00 | 0.90 | 1.50 | 3.00 | 2.50 | 3.50 |
A. ![]() 是自变量,
是自变量,![]() 是因变量
是因变量
B. 2月份这种蔬菜价格最高,为5.50元/千克
C. 2-8月份这种蔬菜价格一直在下降
D. 8-12月份这种蔬菜价格一直在上升