题目内容
【题目】如图,矩形ABCD中,AB=m,AD=n.
(1)若m=4,矩形ABCD的边CD上是否存在点P,使得∠APB=90°?写出点P存在或不存在的可能情况和此时n满足的条件.
(2)矩形ABCD的边上是否存在点P,使得∠APB=60°?写出点P存在或不存在的可能情况和此时m、n满足的条件.


【答案】(1)①当0<n<2时,CD上存在2个点P,使得∠APB=90°;②当n=2时,CD上存在1个点P,使得∠APB=90°;③当n>2时,CD上不存在满足条件的点P;(2)详见解析.
【解析】
(1)根据直角的定义与矩形的关系作图即可分析;
(2)根据含30°的直角三角形的性质结合图形即可求解.
(1)①如图,当0<n<2时,CD上存在2个点P,使得∠APB=90°;
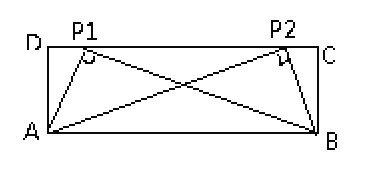
②如图当n=2时,CD上存在1个点P,使得∠APB=90°;
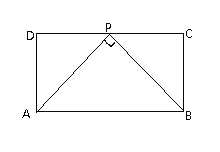
③如图当n>2时,CD上不存在满足条件的点P.
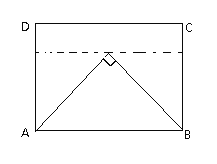
(2)①如图,当![]() =tan60°=
=tan60°=![]() 时,n=
时,n=![]() m时,矩形ABCD的边上存在2个点P,使得∠APB=60°;
m时,矩形ABCD的边上存在2个点P,使得∠APB=60°;
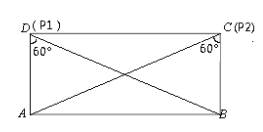
②故当n<![]() m时,矩形ABCD的边上不存在点P,使得∠APB=60°;
m时,矩形ABCD的边上不存在点P,使得∠APB=60°;
③如图,当△ABP为等边三角形时,当![]() =tan60°=
=tan60°=![]() ,即n=
,即n=![]() m时,矩形ABCD的边上存在3个点P,使得∠APB=60°;
m时,矩形ABCD的边上存在3个点P,使得∠APB=60°;
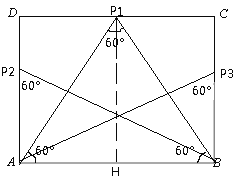
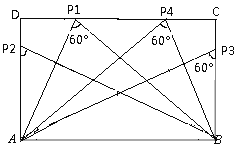
④如图,故当![]() m<n<
m<n<![]() m时,矩形ABCD的边上存在4个点P,使得∠APB=60°;
m时,矩形ABCD的边上存在4个点P,使得∠APB=60°;
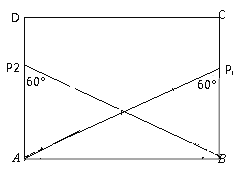
⑤如图,当n>![]() m时,矩形ABCD的边上存在2个点P,使得∠APB=60°.
m时,矩形ABCD的边上存在2个点P,使得∠APB=60°.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目