题目内容
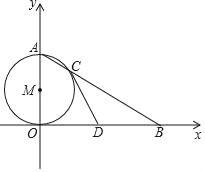
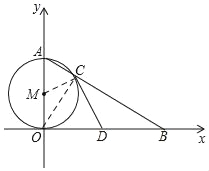
【题目】如图,OA是⊙M的直径,点B在x轴上,连接AB交⊙M于点C.
(1)若点A的坐标为(0,2),∠ABO=30°,求点B的坐标.
(2)若D为OB的中点,求证:直线CD是⊙O的切线.
【答案】(1)B(2![]() ,0);(2)见解析
,0);(2)见解析
【解析】分析:(1)由点A的坐标可知OA的长度,根据∠ABO的度数可知AB的长度为4,利用勾股定理即可求出OB的长度,从而求出B的坐标.
(2)连接OC、MC、证明∠OCB为直角,根据D为OB的中点,可知∠DCO=∠DOC,易知∠OCM=∠COM,所以∠MCO+∠DCO=∠MCD=90°,即可求证MC⊥CD.
详解:(1)∵A的坐标为(0,2)
∴OA=2,
∵∠ABO=30°,∠AOB=90°,
∴AB=2OA=4,
∴由勾股定理可知:OB=2![]() ,
,
∴B(2![]() ,0)
,0)
(2)连接OC,MC
∵OA是⊙M的直径,
∴∠ACO=90°,
∴∠OCB=90°,
在Rt△OCB中,D为OB的中点,
∴CD=![]() OB=OD,
OB=OD,
∴∠DCO=∠DOC,
∵MC=MO,
∴∠OCM=∠COM
∵∠MOC+∠DOC=∠AOB=90°,
∴∠MCO+∠DCO=∠MCD=90°
即MC⊥CD
∴直线CD是⊙M的切线.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目