题目内容
【题目】已知关于x、y的方程组![]() 的解都小于1,若关于a的不等式组
的解都小于1,若关于a的不等式组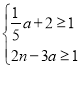 恰好有三个整数解;
恰好有三个整数解;
⑴ 分别求出m与n的取值范围;
⑵请化简:![]() 。
。
【答案】(1)![]() (2)2m-2n-6
(2)2m-2n-6
【解析】
(1)解关于x、y的不等式组,得﹣3<m<1 .同理可以得出﹣5≤a≤![]() . 由于原不等式组恰好有三个整数解,则-3≤
. 由于原不等式组恰好有三个整数解,则-3≤![]() <-2,解得-4≤n<﹣
<-2,解得-4≤n<﹣![]() .
.
(2)由m、n的取值范围得出m+3>0,1﹣m>0,2n+8>0,从而化简得出最后结果.
(1)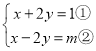 ,
,
①+②得:2x=m+1,即x=![]() <1;
<1;
①﹣②得:4y=1﹣m,即y=![]() <1,
<1,
解得:﹣3<m<1;
由![]() a+2≥1得a≥﹣5,
a+2≥1得a≥﹣5,
2n-3a≥1得a≤![]() .
.
所以﹣5≤a≤![]() .
.
原不等式组恰好有三个整数解,则-3≤![]() <-2,
<-2,
解得-4≤n<﹣![]() .
.
(2)∵﹣3<m<1,![]()
∴m+3>0,1﹣m>0,2n+8>0
原式=m+3﹣(1-m)-(2n+8)=2m-2n-6.

练习册系列答案
相关题目