Question

【题目】在ABCD中，对角线AC，BD相交于点O．EF过点O且与ABCD分别相交于点E，F

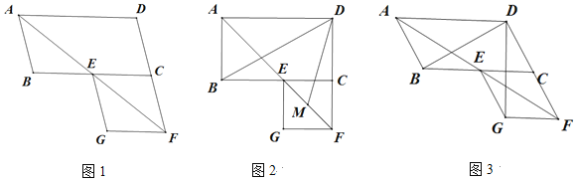
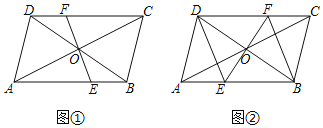
（1）如图①，求证：OE=OF；

（2）如图②，若EF⊥DB，垂足为O，求证：四边形BEDF是菱形．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

(1)由四边形ABCD是平行四边形，得到OB=OD，AB∥CD，根据全等三角形的性质即可得到结论；

(2)根据对角线互相平分的四边形是平行四边形先判定四边形BEDF是平行四边形，继而根据对角线互相垂直的平行四边形是菱形即可得结论.

(1)∵四边形ABCD是平行四边形，

∴OB=OD，AB∥CD，

∴∠EBO=∠FDO，

在△OBE与△ODF中，，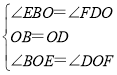

∴△OBE≌△ODF(ASA)，

∴OE=OF；

(2)∵OB=OD，OE=OF，

∴四边形BEDF是平行四边形，

∵EF⊥BD，

∴平行四边形BEDF是菱形．