��Ŀ����
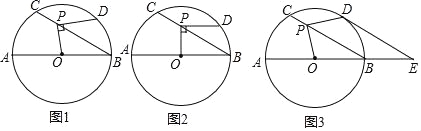
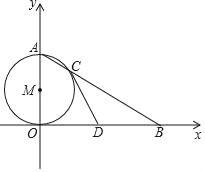
����Ŀ����1����ͼ����֪����![]() �У���
����![]() �DZ�
�DZ�![]() �ϵ�һ���㣨�����
�ϵ�һ���㣨�����![]() ��
��![]() �غϣ�������
�غϣ�������![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() �������߶�
�������߶�![]() ����֮�����������������ϵ����֤����IJ��룻
����֮�����������������ϵ����֤����IJ��룻
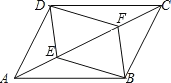
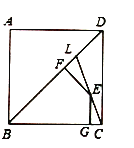
��2����ͼ������![]() �ھ���
�ھ���![]() �ı�
�ı�![]() ���ӳ����ϣ�����
���ӳ����ϣ�����![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() �����߶�
�����߶�![]() ����֮�����������������ϵ��ֱ��д����Ľ��ۣ�
����֮�����������������ϵ��ֱ��д����Ľ��ۣ�
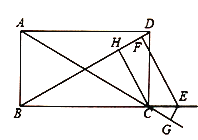
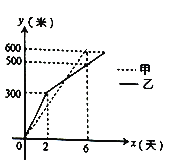
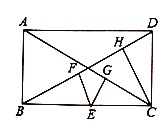
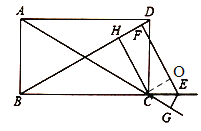
��3����ͼ��![]() ��������
��������![]() �ĶԽ��ߣ�
�ĶԽ��ߣ�![]() ��
��![]() �ϣ���
�ϣ���![]() ������
������![]() ����
����![]() ��
��![]() ����һ�㣬
����һ�㣬![]() ���
���![]() ��
��![]() �ڵ�
�ڵ�![]() �������߶�
�������߶�![]() ֮�����������������ϵ��ֱ��д����IJ���.
֮�����������������ϵ��ֱ��д����IJ���.
���𰸡���1��![]() ������������2��
������������2��![]() ����
����![]() ������������3��
������������3��![]() .
.
��������
��1����![]() ����
����![]() ��
��![]() ,�ȵó��ı���
,�ȵó��ı���![]() �Ǿ��Σ���֤���ı���
�Ǿ��Σ���֤���ı���![]() �Ǿ��Σ�֤��
�Ǿ��Σ�֤��![]() �����
�����![]() ���ɣ�
���ɣ�
��2����C����CO��ֱEF,�ɵþ���HCOF,��ΪHC=FO,ֻҪ֤��EO=EG��������AAS֤��![]() .
.
��3������AC��BD��O,����E��EH��AC,֤������FOHE,֤��EG=CH,����AAS֤��![]() .
.
��1����![]()
֤������ͼ1����![]() ����
����![]() ��
��![]() ��
��
![]() ��
��

![]() �ı���
�ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
![]() ��
��
![]() ��
��
![]() �ı���
�ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
![]() ���һ���ƽ��
���һ���ƽ��
���DBC=��ACB
![]()
![]() ��
��
![]() ��
��
��![]() ��
��
![]() ��
��
��EG=CN
![]() ��
��
��![]() ��
��
��2��![]() ����
����![]() ��
��
��C����CO��ֱEF,
��![]() ��CO��EF��
��CO��EF��![]()
�����COHF
��CE��BD��CH=DO
���DBC=��OCE
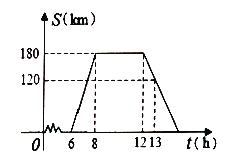
�߾���ABCD
���DBC=��ACB
�ߡ�ECG=��ACB
���ECG=��OCE
��CO��EF��![]()
���G=��COE
��CE=CE
��![]()
��EO=EG
��![]() ����
����![]() ��
��
��3��![]() .
.

����AC��BD��O,����E��EH��AC,
��������ABCD
��FO��AC,![]()
��EH��AC
�����FEOH,��EHC=90��
��EG��BC��EF=OH
���EGC=90��=��EHC
��EH��BD
���HEC=��FLE
��BL=BC
���GCE=��FLE
���GCE=��HEC
��EC=EC
��![]()
��HC=GE
��![]()

 ��У����ϵ�д�
��У����ϵ�д�