题目内容
【题目】已知正方形的每个角等于90°,请解决下列问题:
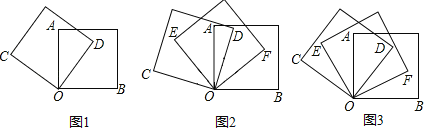
(1)如图1,将两个正方形的一个顶点O重合放置,若∠AOD=50°,求∠COB的度数;
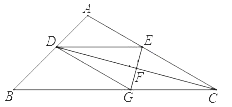
(2)如图2,将三个正方形的一个顶点O重合放置,若∠EOC=40°,∠BOF=30°,求∠AOD的度数;
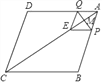
(3)如图3,将三个正方形的一个顶点O重合放置,若OF平分∠DOB,那么OE平分∠AOC吗?为什么?
【答案】(1)∠COB=130°;(2)∠AOD=20°;(3) OE平分∠AOC,证明见解析.
【解析】
(1)根据正方形各角等于90°,得出∠COD+∠AOB=180°,再根据∠AOD=50°,∠COB=∠COD+∠AOB﹣∠AOD,即可得出答案;
(2)根据已知得出∠1+∠2,∠1+∠3的度数,再根据∠1+∠2+∠3=90°,最后用∠1+∠2+∠1+∠3﹣(∠1+∠2+∠3),即可求出∠1的度数;
(3)根据∠COD=∠AOB和等角的余角相等得出∠COA=∠DOB,∠EOA=∠FOB,再根据角平分线的性质得出∠DOF=∠FOB=![]() ∠DOB和∠EOA=
∠DOB和∠EOA=![]() ∠DOB=
∠DOB=![]() ∠COA,从而得出答案.
∠COA,从而得出答案.
(1)∵两个图形是正方形,
∴∠COD=90°,∠AOB=90°,
∴∠COD+∠AOB=180°,
∵∠AOD=50°,
∴∠COB=∠COD+∠AOB﹣∠AOD=130°;
(2) 如图:∵∠COD=90°,∠AOB=90°,∠EOF=90°,
∴∠COE+∠2+∠1=90°,∠2+∠1+∠3=90°,∠1+∠2+∠BOF=90°,
又∵∠EOC=40°,∠BOF=30°,
∴∠1+∠2=50°①,∠1+∠3=60°②,
又∠1+∠2+∠3=90°③,
①+②﹣③得:∠1=20°;
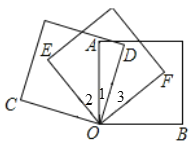
(3)OE平分∠AOC,理由如下:
∵∠COD=∠AOB=90°,
∴∠COD-∠AOD=∠AOB-∠AOD,
即∠COA=∠DOB,
同理:∠EOA=∠FOB,
∵OF平分∠DOB,
∴∠DOF=∠FOB=![]() ∠DOB,
∠DOB,
∴∠EOA=![]() ∠DOB=
∠DOB=![]() ∠COA,
∠COA,
∴OE平分∠AOC.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案