题目内容
如图,在正方形ABCD中,F是CD上一点,AE⊥AF,点E在CB的延长线上,EF交AB于点G.求证:DF•FC=BG•EC.
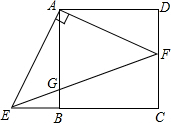

证明:∵∠EAB+∠BAF=90°,∠DAF+∠BAF=90°,
∴∠BAE=∠DAF,
∴tan∠BAE=tan∠DAF,
∵AB=AD,
∴DF=BE,
又∵AB∥CD,
∴
=
,
∴BE•FC=BG•EC,
∴DF•FC=BG•EC.
∴∠BAE=∠DAF,
∴tan∠BAE=tan∠DAF,
∵AB=AD,
∴DF=BE,
又∵AB∥CD,
∴
| BE |
| EC |
| BG |
| FC |
∴BE•FC=BG•EC,
∴DF•FC=BG•EC.

练习册系列答案
相关题目