题目内容

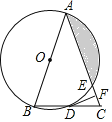
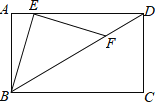
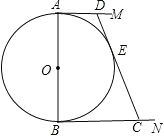
【题目】如图，⊙O的直径是AB=12cm,AM、BN是它的两条切线，DE与⊙O相切于点E，并与AM、BN分别相交于D、C两点，设AD=x,BC=y，则y与x的函数解析式为______.

【答案】y=

【解析】

作出辅助线构造直角三角形，运用勾股定理及切线的性质定理即可求出y关于x的函数解析式.

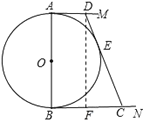
如图，过点D作DF⊥BC于点F，

∵AD、BC是它的两条切线，

∴∠OAD=∠OBF=90°

又DF⊥BC，

∴四边形ABFD为矩形，

∴DF=AB=12cm，BF=AD，

∵AD、BC、DC分别是圆O的切线，

∴DF=DA=x,CE=CB=y，CF=y-x；

∴DC=x+y

由勾股定理得DC2=DF2+CF2

即（x+y）2=(y-x)2+122,

整理得xy=36，

∴y=

练习册系列答案
相关题目

【题目】如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①b2＞4ac；②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；③当y＞0时，x的取值范围是﹣1＜x≤3；④当x＞0时，y随x增大而增大．⑤a＞-c上述五个结论中正确的有_________（填序号）

【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC、AC交于点D、E，过点D作DF⊥AC于点F．

（1）若⊙O的半径为3，∠CDF=15°，求阴影部分的面积；

（2）求证：DF是⊙O的切线；

（3）求证：∠EDF=∠DAC．

【题目】如图①，二次函数的图像与轴交于、两点（点在的左侧），顶点为，连接并延长交轴于点，若.

（1）求二次函数的表达式；

（2）在轴上方有一点，，且，连接并延长交抛物线于点，求点的坐标；

（3）如图②，折叠△，使点落在线段上的点处，折痕为．若△ 有一条边与轴垂直，直接写出此时点的坐标．

【题目】某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动，学校收集整理数据后，将减压方式分为五类，并绘制了图1、图2两个不完整的统计图，请根据图中的信息解答下列问题：

九年级接受调查的同学共有多少名，并补全条形统计图；

九年级共有500名学生，请你估计该校九年级听音乐减压的学生有多少名；

若喜欢“交流谈心”的5名同学中有三名男生和两名女生，心理老师想从5名同学中任选两名同学进行交流，请用画树状图或列表的方法求同时选出的两名同学都是女生的概率．

【题目】.如图，⊙O是△ABC的外接圆，直线DE是⊙O的切线，点A为切点，DE∥BC；

（1）如图1.求证：AB=AC；

（2）如图2.点P是弧AB上一动点，连接PA、PB，作PF⊥PB,垂足为点P,PF交⊙O于点F, 求证：∠BAC=2∠APF；

（3）如图3.在（2）的条件下，连接PC，PA=，PB=，PC=，求线段PF的长.

【题目】如图，在平行四边形ABCD中，，延长DA于点E，使得，连接BE．

求证：四边形AEBC是矩形；

过点E作AB的垂线分别交AB，AC于点F，G，连接CE交AB于点O，连接OG，若，，求的面积．

【题目】在矩形ABCD中，，，点E在射线DA上，连接BE，将线段BE绕点E旋转后，点B恰好落在射线DB上此时点B的对应点为点，则线段DF的长为______．

【题目】某校要求200名学生进行社会调查，每人必须完成份报告，调查结束后随机抽查了20名学生每人完成报告的份数，并分为四类，A：3份；B：4份；C：5份；D：6份，将各类的人数绘制成扇形图如图和尚未完整的条形图如图，回答下列问题：

请将条形统计图2补充完整；

写出这20名学生每天完成报告份数的众数______份和中位数______份；

在求出20名学生每人完成报告份数的平均数时，小明是这样分析的：

第一步：求平均数的公式是；

第二步：在该问题中，，，，，；

第三步：(份)；

小明的分析对不对？如果对，请说明理由，如果不对，请求出正确结果．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网