Question

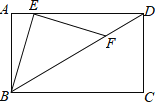
【题目】在矩形ABCD中，，，点E在射线DA上，连接BE，将线段BE绕点E旋转后，点B恰好落在射线DB上此时点B的对应点为点，则线段DF的长为______．

Answer 1

【答案】或105

【解析】

解直角三角形得到AD＝12，过F作FH⊥AD于H，设DH＝4x，FH＝3x，根据勾股定理得到DF＝5x，根据余角的性质得到∠ABE＝∠HEF，根据全等三角形的性质得到AE＝HF＝3x，EH＝AB＝9，分情况讨论列方程即可得到结论．

如图1，∵四边形ABCD是矩形，

∴∠A＝90°，

∵AB＝9，tan∠ADB＝ ，

∴AD＝12，

过F作FH⊥AD于H，

∵tan∠ADB＝，

∴设DH＝4x，FH＝3x，

∴DF＝5x，

∵∠BEF＝90°，

∴∠ABE+∠AEB＝∠AEB+∠HEF＝90°，

∴∠ABE＝∠HEF，

在△ABE与△HEF中， ，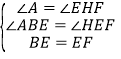

∴△ABE≌△HEF（AAS），

∴AE＝HF＝3x，EH＝AB＝9，

∴AE+DH＝AD﹣EH＝3x+4x＝12﹣9＝3，

∴x＝ ，

∴DF＝5x＝ ；

如图2，∵四边形ABCD是矩形，

∴∠BAD＝90°，

∵AB＝9，tan∠ADB＝，

∴AD＝12，

过F作FH⊥AD于H，

∵tan∠ADB＝，

∴设DH＝4x，FH＝3x，

∴DF＝5x，

∵∠BEF＝90°，

∴∠ABE+∠AEB＝∠AEB+∠HEF＝90°，

∴∠ABE＝∠HEF，

在△ABE与△HEF中，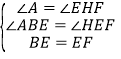

∴△ABE≌△HEF，

∴AE＝HF＝3x，EH＝AB＝9，

∴DH﹣AE＝AD+EH＝4x﹣3x＝12+9＝21，

∴x＝21，

∴DF＝5x＝105，

综上所述，线段DF的长为 或105．

故答案为：或105．