Question

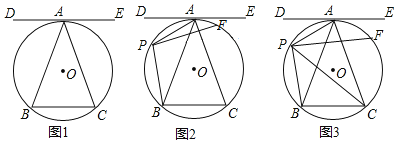
【题目】.如图，⊙O是△ABC的外接圆，直线DE是⊙O的切线，点A为切点，DE∥BC；

（1）如图1.求证：AB=AC；

（2）如图2.点P是弧AB上一动点，连接PA、PB，作PF⊥PB,垂足为点P,PF交⊙O于点F, 求证：∠BAC=2∠APF；

（3）如图3.在（2）的条件下，连接PC，PA=，PB=，PC=，求线段PF的长.

Answer 1

【答案】（1）见解析；（2）见解析；（3）.

【解析】

（1）如图1中，连接OA，延长AO交BC于H，只需证明AH垂直平分BC即可；（2）如图2中，连接OA、BF，首先证明BF是直径，可得∠1=∠3，再证明OA平方∠BAC即可解决问题；（3）如图3中，连接AF、CF、BF、OA延长OA交BC于H，在AB上取一点K，使得∠BPK=∠APC，作BM⊥PC于M，利用△APC∽△KPB和△APK∽△CPB推出，设BC=k，AB=AC=k，⊙O的半径为r，在Rt△ABH中，AH=k，在Rt△OBH中，OB2=OH2+BH2，得到r2=（k）2+（k-r）2，推出r=k，在Rt△FBC中，sin∠BFC=，推出cos∠BFC=，在Rt△PBM中，PB=5，由∠BPC=∠BFC，推出PM=PBcos∠PBC=×5=4，BM=PBsin∠BPC=5×=3，CM=PC=PM=3，
推出BM=CM=3，则BC=CM=6，可得k=6，求得k=3，求出半径即可解决问题.

（1）证明：如图1中，连接OA，延长AO交BC于H．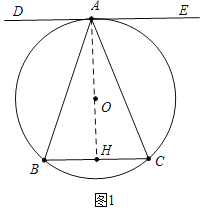

∵DE是切线，
∴OA⊥DE，
∵DE∥BC，
∴AH⊥BC，
∴BH=CH，
∴AB=AC．
（2）证明：如图2中，连接OA、BF．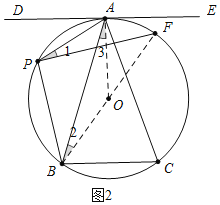

∵BP⊥PF，
∴∠BPF=90°，
∴BF是直径，
∵OB=OA，
∴∠2=∠3，
∵∠1=∠2，
∴∠1=∠3，
由（1）可知，AB=AC，AO⊥BC，
∴OA平分∠BAC，
∴∠BAC=2∠3=2∠1，
∴∠BAC=2∠APF．
（3）解：如图3中，连接AF、CF、BF、OA延长OA交BC于H，在AB上取一点K，使得∠BPK=∠APC，作BM⊥PC于M．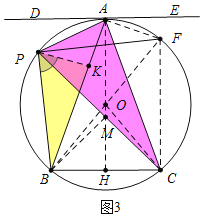

∵∠BPK=∠APC，∠AFP=∠PBK，
∴△APC∽△KPB，
∴PBAC=BKPC ①
∵∠APK=∠CPB，∠PAK=∠PCB，
∴△APK∽△CPB，
∴PABC=PCAK ②，
①+②得PBAC+PABC=PCAB，
∵AB=AC，
∴，

设BC=k，AB=AC=k，⊙O的半径为r．
在Rt△ABH中，AH==k，
在Rt△OBH中，∵OB2=OH2+BH2，
∴r2=（k）2+（k-r）2，
∴r=k，
在Rt△FBC中，sin∠BFC=，
∴cos∠BFC=，
在Rt△PBM中，∵PB=5，∠BPC=∠BFC，
∴PM=PBcos∠PBC=×5=4，BM=PBsin∠BPC=5×=3，
∴CM=PC=PM=3，
∴BM=CM=3，
∴BC=CM=6，
∴k=6，
∴k=3，
∴r=×3=5，
在Rt△PBF中，PF==5．