题目内容
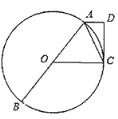
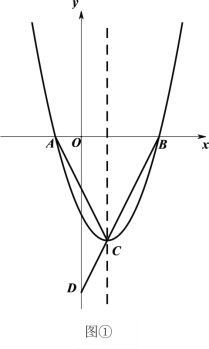
【题目】如图①,二次函数![]() 的图像与
的图像与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在
在![]() 的左侧),顶点为
的左侧),顶点为![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,若
,若![]() .
.
(1)求二次函数的表达式;
(2)在![]() 轴上方有一点
轴上方有一点![]() ,
,![]() ,且
,且![]() ,连接
,连接![]() 并延长交抛物线于点
并延长交抛物线于点![]() ,求点
,求点![]() 的坐标;
的坐标;
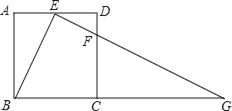
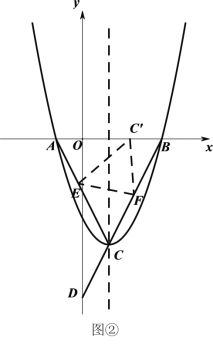
(3)如图②,折叠△![]() ,使点
,使点![]() 落在线段
落在线段![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() .若△
.若△![]() 有一条边与
有一条边与![]() 轴垂直,直接写出此时点
轴垂直,直接写出此时点![]() 的坐标.
的坐标.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 、
、![]()
【解析】
(1)函数的对称轴为x![]() 1,BC=2CD,xB=3xC=3,即B的坐标为(3,0),即可求解;
1,BC=2CD,xB=3xC=3,即B的坐标为(3,0),即可求解;
(2)易证HMA≌△ANC(AAS),则AM=NC=2,MH=AN=4,可求出点H的坐标和直线CH的表达式,将该表达式与二次函数表达式联立,即可求解;
(3)分C'F⊥x轴、EC'⊥x轴,两种情况求解即可.
(1)函数的对称轴为x![]() 1,BC=2CD,xB=3xC=3,即B的坐标为(3,0),将点B的坐标代入二次函数表达式得:
1,BC=2CD,xB=3xC=3,即B的坐标为(3,0),将点B的坐标代入二次函数表达式得:
0=a×32﹣2a×3﹣3,解得:a=1.
故二次函数的表达式为:y=x2﹣2x﹣3…①,则顶点C的坐标为(1,﹣4),令y=0,则x=﹣1或3,即点A的坐标为(﹣1,0);
(2)过点A作MN∥y轴,分别过点H、C作HM⊥MN、CN⊥MN于点M、N,如图1.
∵∠MAH+∠NAC=90°,∠NAC+∠ACN=90°,∴∠MAH=∠ACN,∠HMA=∠CNA=90°,AC=AH,∴△HMA≌△ANC(AAS),∴AM=NC=2,MH=AN=4,∴点H的坐标为(3,2),设直线HC的解析式为:y=mx+n,把H、C的坐标代入得:![]() ,解得:
,解得:![]() ,故直线CH的表达式为:y=3x﹣7…②,联立①②并解得:
,故直线CH的表达式为:y=3x﹣7…②,联立①②并解得:![]() 或
或![]() ,即点P的坐标为(4,5);
,即点P的坐标为(4,5);
(3)①当C'F⊥x轴,设:函数对称轴交x轴于点G,如图2,则tan∠GBC![]() ,设:BC'=x,则FC'=2x=FC,则BF
,设:BC'=x,则FC'=2x=FC,则BF![]() x,BC=BF+CF=2x
x,BC=BF+CF=2x![]() ,即:x=10﹣4
,即:x=10﹣4![]() ,∴点C'的坐标为(4
,∴点C'的坐标为(4![]() 7,0);
7,0);


②当EC'⊥x轴,同理可得点C'的坐标为:(9﹣4![]() ,0).
,0).
综上所述:点C'的坐标为(4![]() 7,0)或(9﹣4
7,0)或(9﹣4![]() ,0).
,0).

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案