Question

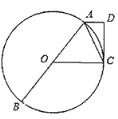
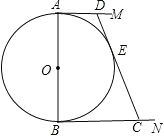
【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O分别与BC、AC交于点D、E，过点D作DF⊥AC于点F．

（1）若⊙O的半径为3，∠CDF=15°，求阴影部分的面积；

（2）求证：DF是⊙O的切线；

（3）求证：∠EDF=∠DAC．

Answer 1

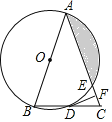
【答案】（1）阴影部分的面积为3π﹣；（2）证明见解析；（3）证明见解析.

【解析】（1）连接OE，过O作OM⊥AC于M，求出AE、OM的长和∠AOE的度数，分别求出△AOE和扇形AOE的面积，即可求出答案；

（2）连接OD，求出OD⊥DF，根据切线的判定求出即可；

（3）连接BE，求出∠FDC=∠EBC，∠FDC=∠EDF，即可求出答案．

详（1）解： 连接OE，过O作OM⊥AC于M，则∠AMO=90°，

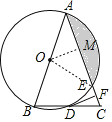
∵DF⊥AC，

∴∠DFC=90°，

∵∠FDC=15°，

∴∠C=180°-90°-15°=75°，

∵AB=AC，

∴∠ABC=∠C=75°，

∴∠BAC=180°-∠ABC∠C=30°，

∴OM=OA=×3=，AM=OM=，

∵OA=OE，OM⊥AC，

∴AE=2AM=3，

∴∠BAC=∠AEO=30°，

∴∠AOE=180°-30°-30°=120°，

∴阴影部分的面积S=S扇形AOE-S△AOE=；

（2）证明：连接OD，

∵AB=AC，OB=OD，

∴∠ABC=∠C，∠ABC=∠ODB，

∴∠ODB=∠C，

∴AC∥OD，

∵DF⊥AC，

∴DF⊥OD，

∵OD过O，

∴DF是⊙O的切线；

（3）证明：连接BE，

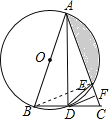
∵AB为⊙O的直径，

∴∠AEB=90°，

∴BE⊥AC，

∵DF⊥AC，

∴BE∥DF，

∴∠FDC=∠EBC，

∵∠EBC=∠DAC，

∴∠FDC=∠DAC，

∵A、B、D、E四点共圆，

∴∠DEF=∠ABC，

∵∠ABC=∠C，

∴∠DEC=∠C，

∵DF⊥AC，

∴∠EDF=∠FDC，

∴∠EDF=∠DAC．