题目内容
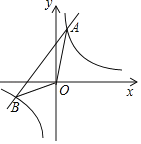
【题目】如图,点A、B是双曲线y=![]() (k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx﹣k﹣1=0的两根
(k为正整数)与直线AB的交点,且A、B两点的横坐标是关于x的方程:x2+kx﹣k﹣1=0的两根
(1)填表:
k | 1 | 2 | 3 | … | n(n为正整数) |
A点的横坐标 |
|
|
|
|
|
B点的横坐标 |
|
|
|
|
|
(2)当k=n(n为正整数)时,试求直线AB的解析式(用含n的式子表示);
(3)当k=1、2、3、…n时,△ABO的面积,依次记为S1、S2、S3…Sn,当Sn=40时,求双曲线y=![]() 的解析式.
的解析式.
【答案】(1)1,1,1,…,1;﹣2,﹣3,﹣4,…,﹣n﹣1(2)y=x+n(3)y=![]()
【解析】
(1)根据k的值,即可得到一元二次方程的解,进而得到A点的横坐标,B点的横坐标;(2)根据当k=n(n为正整数)时,A点的横坐标为1,B点的横坐标为﹣n﹣1,可得A(1,n+1),B(﹣n﹣1,﹣1),运用待定系数法即可得出直线AB的解析式;(3)先求得直线AB与y轴交于(0,n),再根据当Sn=40时,![]() ×n(n+1+1)=40,即可得到n=8,进而得出A(1,9),据此可得双曲线的解析式为y=
×n(n+1+1)=40,即可得到n=8,进而得出A(1,9),据此可得双曲线的解析式为y=![]() .
.
(1)当k=1时,方程x2+x﹣2=0的解为:x1=1,x2=﹣2;
当k=2时,方程x2+2x﹣3=0的解为:x1=1,x2=﹣3;
k=3时,方程x2+3x﹣4=0的解为:x1=1,x2=﹣4;
k=n时,方程x2+nx﹣n﹣1=0的解为:x1=1,x2=﹣n﹣1;
∵点A在第一象限,点B在第三象限,
∴A点的横坐标依次为:1,1,1,…,1;
B点的横坐标依次为:﹣2,﹣3,﹣4,…,﹣n﹣1;
故答案为:1,1,1,…,1;﹣2,﹣3,﹣4,…,﹣n﹣1;
(2)当k=n(n为正整数)时,A点的横坐标为1,B点的横坐标为﹣n﹣1,
令x=1,则y=![]() =n+1;
=n+1;
令x=﹣n﹣1,则y=![]() =﹣1;
=﹣1;
∴A(1,n+1),B(﹣n﹣1,﹣1),
设直线AB的解析式为y=px+q,则
![]() ,
,
解得![]() ,
,
∴直线AB的解析式为y=x+n;
(3)∵直线y=x+n中,令x=0,则y=n,即直线AB与y轴交于(0,n),
∴当Sn=40时,![]() ×n(n+1+1)=40,
×n(n+1+1)=40,
解得n=8(负值已舍去),
∴A(1,9),
∴双曲线的解析式为:y=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
从上表可知,下列说法正确的有多少个
①抛物线与x轴的一个交点为(﹣2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是直线x=![]() ;
;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减少.
A. 2 B. 3 C. 4 D. 5