题目内容
【题目】某校九(18)班开展数学活动,毓齐和博文两位同学合作用测角仪测量学校的旗杆,毓齐站在B点测得旗杆顶端E点的仰角为45°,博文站在D(D点在直线FB上)测得旗杆顶端E点仰角为15°,已知毓齐和博文相距(BD)30米,毓齐的身高(AB)1.6米,博文的身高(CD)1.75米,求旗杆的高EF的长.(结果精确到0.1)
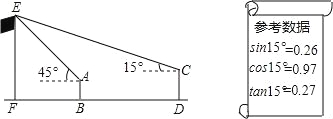
【答案】旗杆的高EF为12.9米
【解析】
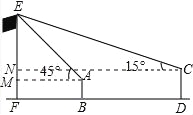
试题分析:过点A作AM⊥EF于M,过点C作CN⊥EF于N,则MN=0.15米,根据E点的仰角为45°,可得△AEM是等腰直角三角形,得出AM=ME,设AM=ME=x米,则CN=(x+30)米,EN=(x﹣0.15)米,在Rt△CEN中,由tan∠ECN=![]() ,代入CN、EN解方程求出x的值,继而可求得旗杆的高EF的长.
,代入CN、EN解方程求出x的值,继而可求得旗杆的高EF的长.
试题解析:过点A作AM⊥EF于M,过点C作CN⊥EF于N,
∵AB=1.6米,CD=1.75米,
∴MN=0.15米,
∵∠EAM=45°,
∴AM=ME,
设AM=ME=x米,
∵BD=30米
∴CN=(x+30)米,EN=(x﹣0.15)米,
∵∠ECN=15°,
∴tan∠ECN=![]() =
=![]() ,
,
解得:x≈11.3,
则EF=EM+MF=11.3+1.6=12.9(米).
答:旗杆的高EF为12.9米.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目