Question

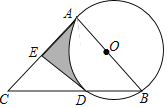
【题目】如图，AB是⊙O的直径，AC是⊙O的切线，切点为A，BC交⊙O于点D，点E是AC的中点．

（1）试判断直线DE与⊙O的位置关系，并说明理由；

（2）若⊙O的半径为2，∠B=50°，AC=4.8，求图中阴影部分的面积．

Answer 1

【答案】（1）直线DE与⊙O相切．理由见解析；（2）图中阴影部分的面积为4.8﹣π．

【解析】（1）连接OE、OD，如图，根据切线的性质得∠OAC=90°，再证明△AOE≌△DOE得到∠ODE=∠OAE=90°，然后根据切线的判定定理得到DE为⊙O的切线；

（2）先计算出∠AOD=2∠B=100°，利用四边形的面积减去扇形的面积计算图中阴影部分的面积．

（1）直线DE与⊙O相切．理由如下：

连接OE、OD，如图，

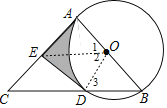
∵AC是⊙O的切线，

∴AB⊥AC，

∴∠OAC=90°，

∵点E是AC的中点，O点为AB的中点，

∴OE∥BC，

∴∠1=∠B，∠2=∠3，

∵OB=OD，

∴∠B=∠3，

∴∠1=∠2，

在△AOE和△DOE中

，

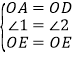∴△AOE≌△DOE，

∴∠ODE=∠OAE=90°，

∴OA⊥AE，

∴DE为⊙O的切线；

（2）∵点E是AC的中点，

∴AE=AC=2.4，

∵∠AOD=2∠B=2×50°=100°，

∴图中阴影部分的面积=2××2×2.4﹣．