题目内容
【题目】如图,已知BD是△ABC的角平分线,点E、F分别在边AB、BC上,ED∥BC,EF∥AC.求证:BE=CF. 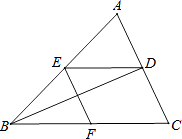
【答案】证明:∵ED∥BC,EF∥AC, ∴四边形EFCD是平行四边形,
∴DE=CF,
∵BD平分∠ABC,
∴∠EBD=∠DBC,
∵DE∥BC,
∴∠EDB=∠DBC,
∴∠EBD=∠EDB,
∴EB=ED,
∴EB=CF.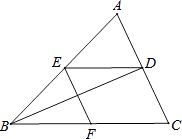
【解析】本题考查平行四边形的判定和性质、等腰三角形的判定和性质等知识,先利用平行四边形性质证明DE=CF,再证明EB=ED,即可解决问题.
【考点精析】根据题目的已知条件,利用平行四边形的判定与性质的相关知识可以得到问题的答案,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






