Question

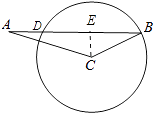
【题目】如图，在△ABC中，已知∠ACB=130°，∠BAC=20°，BC=2，以点C为圆心，CB为半径的圆交AB于点D，则BD的长为 ．

Answer 1

【答案】
【解析】解：如图，作CE⊥AB于E． ∵∠B=180°﹣∠A﹣∠ACB=180°﹣20°﹣130°=30°，
在RT△BCE中，∵∠CEB=90°，∠B=30°，BC=2，
∴CE= BC=1，BE= CE= ，
∵CE⊥BD，
∴DE=EB，
∴BD=2EB=2 ．
故答案为2 ．

如图，作CE⊥AB于E，在RT△BCE中利用30度性质即可求出BE，再根据垂径定理可以求出BD．本题考查垂径定理、三角形内角和定理等知识，解题的关键是根据垂径定理添加辅助线，记住直角三角形30度角性质，属于基础题，中考常考题型．