题目内容
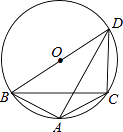
【题目】如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC、AD、OD,其中AC=CD,过点B的切线交CD的延长线于E. 
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长之和(参考数据:π=3.1, ![]() =1.4,
=1.4, ![]() =1.7)
=1.7)
【答案】
(1)证明:∵CD∥AB,
∴∠CDA=∠BAD,
又∵OA=OD,
∴∠ADO=∠BAD,
∴∠ADO=∠CDA,
∴DA平分∠CDO
(2)解:如图:
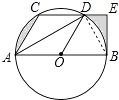 连接BD,
连接BD,
∵AB是直径,
∴∠ADB=90°,
∵AC=CD,
∴∠CAD=∠CDA,
又∵CD∥AB,
∴∠CDA=∠BAD,
∴∠CDA=∠BAD=∠CAD,
∴ ![]() =
= ![]() =
= ![]() ,
,
又∵∠AOB=180°,
∴∠DOB=60°,
∵OD=OB,
∴△DOB是等边三角形,
∴BD=OB= ![]() AB=6,
AB=6,
∵ ![]() =
= ![]() ,
,
∴AC=BD=6,
∵BE切⊙O于B,
∴BE⊥AB,
∴∠DBE=∠ABE﹣∠ABD=30°,
∵CD∥AB,
∴BE⊥CE,
∴DE= ![]() BD=3,BE=BD×cos∠DBE=6×
BD=3,BE=BD×cos∠DBE=6× ![]() =3
=3 ![]() ,
,
∴ ![]() 的长=
的长= ![]() =2π,
=2π,
∴图中阴影部分周长之和为 ![]() =4π+9+3
=4π+9+3 ![]() =4×3.1+9+3×1.7=26.5.
=4×3.1+9+3×1.7=26.5.
【解析】(1)只要证明∠CDA=∠DAO,∠DAO=∠ADO即可.(2)首先证明 ![]() =
= ![]() =
= ![]() ,再证明∠DOB=60°得△BOD是等边三角形,由此即可解决问题.本题考查切线的性质、平行线的性质、等边三角形的判定和性质、弧长公式等知识,解题的关键是灵活应用这些知识解决问题,学会添加常用辅助线,属于中考常考题型.
,再证明∠DOB=60°得△BOD是等边三角形,由此即可解决问题.本题考查切线的性质、平行线的性质、等边三角形的判定和性质、弧长公式等知识,解题的关键是灵活应用这些知识解决问题,学会添加常用辅助线,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目