题目内容
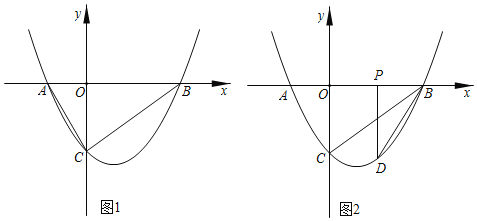
【题目】如图,直线y=![]() x+6与x轴、y轴分别交于A,B两点,将直线l1沿着y轴正方向平移一段距离得到直线l2交y轴于点M,且l1与l2之间的距离为3,点C(x,y)是直线11上的一个动点,过点C作AB的垂线CD交y轴于点D.
x+6与x轴、y轴分别交于A,B两点,将直线l1沿着y轴正方向平移一段距离得到直线l2交y轴于点M,且l1与l2之间的距离为3,点C(x,y)是直线11上的一个动点,过点C作AB的垂线CD交y轴于点D.

(1)求直线l2的解析式;
(2)当C运动到什么位置时,△AOD的面积为21![]() ,求出此时点C的坐标;
,求出此时点C的坐标;
(3)连接AM,将△ABM绕着点M旋转得到△A'B'M',在平面内是否存在一点N.使四边形AMA'N为矩形?若存在,求出点N的坐标:若不存在,请说明理由.
【答案】(1)y=![]() x+6+2
x+6+2![]() ;(2)C(﹣
;(2)C(﹣![]() ,
,![]() );(3)存在,N点在x轴上方时N坐标:(﹣6﹣8
);(3)存在,N点在x轴上方时N坐标:(﹣6﹣8![]() ,6
,6![]() ),N点在x轴下方时N点坐标:(6﹣4
),N点在x轴下方时N点坐标:(6﹣4![]() ,﹣6
,﹣6![]() ).
).
【解析】
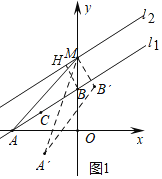
(1)如图1中,作BH⊥直线l2于H.解直角三角形求出点M坐标即可解决问题;
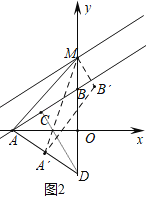
(2)如图2中,连接AD,设D(0,m).利用三角形的面积公式构建方程求出m,再求出直线CD的解析式,利用方程组即可解决问题;
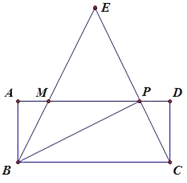
(3)如图3中,分两种情形构造全等三角形解决问题即可.
解:(1)如图1中,作BH⊥直线l2于H.
∵直线y=![]() x+6与x轴、y轴分别交于A,B两点,
x+6与x轴、y轴分别交于A,B两点,
∴B(0,6),A(﹣6![]() ,0),
,0),
∴OB=6,OA=6![]() ,
,
∴tan∠BAO=![]() ,
,
∴∠BAO=30°,
∵∠AOB=90°,
∴∠ABO=60°,
∵BH⊥l2,l1∥l2,
∴BH⊥l1,
∴∠ABH=90°,
∴∠HBM=30°,
∵BH=3,
∴BM=![]() =2
=2![]() ,
,
∴M(0,6+2![]() ),
),
∴直线l2的解析式为y=![]() x+6+2
x+6+2![]() .
.
(2)如图2中,连接AD,设D(0,m).
由题意:![]() ,
,
∴![]() ×
×![]() ×|m|=
×|m|=![]() ,
,
∴m=±7,
∴D(0,7)或(0,﹣7),
当D(0,7)时,∵DC⊥AB,
∴直线CD的解析式为y=﹣![]() x+7,
x+7,
由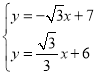 ,解得
,解得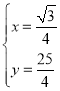 ,
,
∴C(![]() ,
,![]() ).
).
当D(0,﹣7)时,直线CD的解析式为y=﹣![]() x﹣7,
x﹣7,
由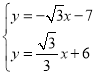 ,解得
,解得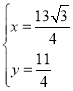 ,
,
∴C(﹣![]() ,
,![]() ).
).
(3)存在, 存在,N点在x轴上方时N坐标:(﹣6﹣8![]() ,6
,6![]() ),N点在x轴下方时N点坐标:(6﹣4
),N点在x轴下方时N点坐标:(6﹣4![]() ,﹣6
,﹣6![]() ),原因如下:
),原因如下:
情况一:当N点在x轴上方时, 如下图,作NH⊥x轴,垂足为点H:
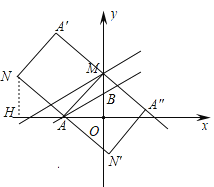
∵四边形AMA′N是矩形,MA=MA′,
∴四边形AMA′N是正方形,
∴AN=AM,
∵∠AHN=∠MAN=∠AOM=90°,
∴∠HAN+∠OAM=90°,∠OAM+∠AMO=90°,
∴∠HAM=∠AMO,
∴△AHN≌△MOA(AAS),
∴NH=OA=6![]() ,AH=OM=6+2
,AH=OM=6+2![]() ,
,
∴OH=6+8![]() ,
,
∴N(﹣6﹣8![]() ,6
,6![]() ),
),
情况二:当点N′在x轴下方时,作N′H′⊥x轴,垂足为点H′:
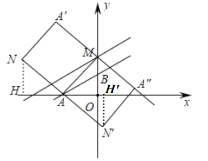
∵四边形AMA′′N′是矩形,MA=MA′′,
∴四边形AMA′′N′是正方形,
∴AN′=AM,
∵∠AH′N′=∠MAN′=∠AOM=90°,
∴∠H′AN′+∠OAM=90°,∠OAM+∠AMO=90°,
∴∠H′AN′=∠AMO,
∴△AH′N′≌△MOA(AAS),
∴N′H′=OA=6![]() ,AH′=OM=6+2
,AH′=OM=6+2![]() ,
,
∴OH=AH′-OA=6-4![]() ,
,
∴N′(6﹣4![]() ,﹣6
,﹣6![]() ).
).
综上所述,存在,N点在x轴上方时N坐标:(﹣6﹣8![]() ,6
,6![]() ),N点在x轴下方时N点坐标:(6﹣4
),N点在x轴下方时N点坐标:(6﹣4![]() ,﹣6
,﹣6![]() ).
).

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案【题目】4月23日,为迎接“世界读书日”,某书城开展购书有奖活动.顾客每购书满100元获得一次摸奖机会,规则为:一个不透明的袋子中装有4个小球,小球上分别标有数字1,2,3,4,它们除所标数字外完全相同,摇匀后同时从中随机摸出两个小球,则两球所标数字之和与奖励的购书券金额的对应关系如下:
两球所标数字之和 | 3 | 4 | 5 | 6 | 7 |
奖励的购书券金额(元) | 0 | 0 | 30 | 60 | 90 |
(1)通过列表或画树状图的方法计算摸奖一次获得90元购书券的概率;
(2)书城规定:如果顾客不愿意参加摸奖,那么可以直接获得30元的购书券.在“参加摸奖”和“直接获得购书券”两种方式中,你认为哪种方式对顾客更合算?请通过求平均教的方法说明理由.