题目内容
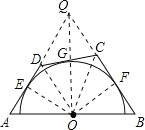
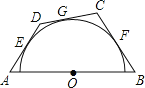
【题目】如图,AB是定长线段,圆心O是AB的中点,AE、BF为切线,E、F为切点,满足AE=BF在![]() 上取动点G,过点G作切线交AE、BF的延长线于点D、C,当点G运动时,设AD=y,BC=x,则y与x所满足的函数关系式为( )
上取动点G,过点G作切线交AE、BF的延长线于点D、C,当点G运动时,设AD=y,BC=x,则y与x所满足的函数关系式为( )
A.正比例函数y=kx(k为常数,k≠0,x>0)B.一次函数y=kx+b(k,b为常数,kb≠0,x>0)
C.二次函数y=ax2+bx+c(a,b,c为常数,a≠0,x>0)D.以上都不是
【答案】D
【解析】
延长AD,BC交于点Q,连接OE,OF,OD,OC,OQ,由AE与BF为圆的切线,利用切线的性质得到AE与EO垂直,BF与OF垂直,由AE=BF,OE=OF,利用HL得到直角三角形AOE与直角BOF全等,利用全等三角形的对应角相等得到∠A=∠B,利用等角对等边可得出三角形QAB为等腰三角形,由O为底边AB的中点,利用三线合一得到QO垂直于AB,得到一对直角相等,再由∠FQO与∠OQB为公共角,利用两对对应角相等的两三角形相似得到三角形FQO与三角形OQB相似,同理得到三角形EQO与三角形OAQ相似,由相似三角形的对应角相等得到∠QOE=∠QOF=∠A=∠B,再由切线长定理得到OD与OC分别为∠EOG与∠FOG的平分线,得到∠DOC为∠EOF的一半,即∠DOC=∠A=∠B,又∠GCO=∠FCO,得到三角形DOC与三角形OBC相似,同理三角形DOC与三角形DAO相似,进而确定出三角形OBC与三角形DAO相似,由相似得比例,将AD=x,BC=y代入,并将AO与OB换为AB的一半,可得出x与y的乘积为定值,即y与x成反比例函数,即可得到正确的选项.
解:延长AD,BC交于点Q,连接OE,OF,OD,OC,OQ,
∵AE,BF为圆O的切线,
∴OE⊥AE,OF⊥FB,
∴∠AEO=∠BFO=90°,
在Rt△AEO和Rt△BFO中,![]() ,
,
∴Rt△AEO≌Rt△BFO(HL),
∴∠A=∠B,
∴△QAB为等腰三角形,
又∵O为AB的中点,即AO=BO,
∴QO⊥AB,
∴∠QOB=∠QFO=90°,
又∵∠OQF=∠BQO,
∴△QOF∽△QBO,
∴∠B=∠QOF,
同理可以得到∠A=∠QOE,
∴∠QOF=∠QOE,
根据切线长定理得:OD平分∠EOG,OC平分∠GOF,
∴∠DOC=![]() ∠EOF=∠A=∠B,
∠EOF=∠A=∠B,
又∵∠GCO=∠FCO,
∴△DOC∽△OBC,
同理可以得到△DOC∽△DAO,
∴△DAO∽△OBC,
![]() ,
,
∴ADBC=AOOB=![]() AB2,即xy=
AB2,即xy=![]() AB2为定值,
AB2为定值,
设k=![]() AB2,得到y=
AB2,得到y=![]() ,
,
则y与x满足的函数关系式为反比例函数y=![]() (k为常数,k≠0,x>0).
(k为常数,k≠0,x>0).
故选:D.