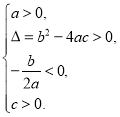题目内容
【题目】4月23日,为迎接“世界读书日”,某书城开展购书有奖活动.顾客每购书满100元获得一次摸奖机会,规则为:一个不透明的袋子中装有4个小球,小球上分别标有数字1,2,3,4,它们除所标数字外完全相同,摇匀后同时从中随机摸出两个小球,则两球所标数字之和与奖励的购书券金额的对应关系如下:
两球所标数字之和 | 3 | 4 | 5 | 6 | 7 |
奖励的购书券金额(元) | 0 | 0 | 30 | 60 | 90 |
(1)通过列表或画树状图的方法计算摸奖一次获得90元购书券的概率;
(2)书城规定:如果顾客不愿意参加摸奖,那么可以直接获得30元的购书券.在“参加摸奖”和“直接获得购书券”两种方式中,你认为哪种方式对顾客更合算?请通过求平均教的方法说明理由.
【答案】(1)![]() ;(2)在“参加摸球”和“直接获得购书券”两种方式中,我认为选择“参加摸球”对顾客更合算,理由见解析.
;(2)在“参加摸球”和“直接获得购书券”两种方式中,我认为选择“参加摸球”对顾客更合算,理由见解析.
【解析】
(1)根据题意,列出表格,然后利用概率公式求概率即可;
(2)先根据(1)中表格计算出两球数字之和的各种情况对应的概率,然后计算出摸球一次平均获得购书券金额,最后比较大小即可判断.
解:(1)列表如下:
第1球 第2球 | 1 | 2 | 3 | 4 |
1 |
|
|
| |
2 |
|
|
| |
3 |
|
|
| |
4 |
|
|
|
由上表可知,共有12种等可能的结果.其中“两球数字之和等于7”有2种,
∴![]() (获得90元购书券)
(获得90元购书券)![]() .
.
(2)由(1)中表格可知,两球数字之和的各种情况对应的概率如下:
数字之和 | 3 | 4 | 5 | 6 | 7 |
获奖金额(元) | 0 | 0 | 30 | 60 | 90 |
相应的概率 |
|
|
|
|
|
∴摸球一次平均获得购书券金额为
![]() 元
元
∵![]() ,
,
∴在“参加摸球”和“直接获得购书券”两种方式中,我认为选择“参加摸球”对顾客更合算.

【题目】关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等且非零的实数根,探究
有两个不相等且非零的实数根,探究![]() 满足的条件.
满足的条件.
小华根据学习函数的经验,认为可以从二次函数的角度研究一元二次方程的根的符号。下面是小华的探究过程:第一步:设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
第二步:借助二次函数图象,可以得到相应的一元二次方程中![]() 满足的条件,列表如下表。
满足的条件,列表如下表。
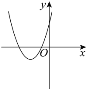
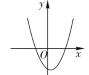
方程两根的情况 | 对应的二次函数的大致图象 |
|
方程有两个不相等的负实根 |
|
|
①_______ |
|
|
方程有两个不相等的正实根 | ② | ③____________ |
(1)请将表格中①②③补充完整;
(2)已知关于![]() 的方程
的方程![]() ,若方程的两根都是正数,求
,若方程的两根都是正数,求![]() 的取值范围.
的取值范围.