Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ◊ŘļŌ”ŽŐĹĺŅ
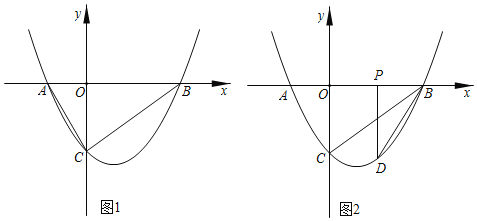
»ÁÕľ1£¨Ň◊őÔŌŖy£Ĺax2+bx©Ā3”Žx÷ŠĹĽ”ŕA£®©Ā2£¨0£©£¨B£®4£¨0£©ŃĹĶ„£¨”Žy÷ŠĹĽ”ŕĶ„C£ģ
£®1£©«ůŇ◊őÔŌŖĶńĪŪīÔ Ĺ£Ľ
£®2£©Ķ„N «Ň◊őÔŌŖ…Ō“ž”ŕĶ„CĶń∂ĮĶ„£¨»Ű°ųNABĶń√śĽż”Ž°ųCABĶń√śĽżŌŗĶ»£¨«ů≥ŲĶ„NĶń◊ÝĪÍ£Ľ
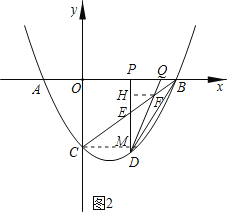
£®3£©»ÁÕľ2£¨ĶĪPő™OBĶń÷–Ķ„ Ī£¨ĻżĶ„P◊ųPD°Õx÷Š£¨ĹĽŇ◊őÔŌŖ”ŕĶ„D£ģѨŔBD£¨Ĺę°ųPBD—ōx÷ŠŌÚ◊ů∆Ĺ“∆młŲĶ•őĽ≥§∂»£®0£ľm°‹2£©£¨Ĺę∆Ĺ“∆Ļż≥Ő÷–°ųPBD”Ž°ųOBC÷ōĶĢ≤Ņ∑÷Ķń√śĽżľ«ő™S£¨«ůS”ŽmĶńļĮ żĻōŌĶ Ĺ£ģ
°ĺīūįł°Ņ£®1£©y£Ĺ![]() x2©Ā
x2©Ā![]() x©Ā3£Ľ£®2£©Ķ„NĶń◊ÝĪÍ «£®
x©Ā3£Ľ£®2£©Ķ„NĶń◊ÝĪÍ «£®![]() +1£¨3£©ĽÚ£®©Ā
+1£¨3£©ĽÚ£®©Ā![]() +1£¨3£©ĽÚ£®2£¨©Ā3£©£Ľ£®3£©S£Ĺ©Ā
+1£¨3£©ĽÚ£®2£¨©Ā3£©£Ľ£®3£©S£Ĺ©Ā![]() m2+
m2+![]() m+
m+![]() £ģ
£ģ
°ĺĹ‚őŲ°Ņ
£®1£©į—Ķ„A°ĘBĶń◊ÝĪÍ∑÷Īūīķ»ŽŇ◊őÔŌŖĹ‚őŲ Ĺ£¨Ń–≥ŲĻō”ŕŌĶ ża°ĘbĶńĹ‚őŲ Ĺ£¨Õ®ĻżĹ‚∑Ĺ≥Ő◊ť«ůĶ√ňŁ√«Ķń÷Ķ£Ľ
£®2£©”…Ň◊őÔŌŖĹ‚őŲ Ĺ«ůĶ√Ķ„CĶń◊ÝĪÍ£¨ľīOC£Ĺ3£¨ňý“‘”…»żĹ«–őĶń√śĽżĻę ĹĶ√ĶĹĶ„NĶĹx÷ŠĶńĺŗņŽő™3£¨ĺ›īňŃ–≥Ų∑Ĺ≥Ő≤ĘĹ‚īū£Ľ
£®3£©»ÁÕľ2£¨”…“—÷™Ķ√£¨QB£Ĺm£¨PQ£Ĺ2£¨ņŻ”√īż∂®ŌĶ ż∑®»∑∂®÷ĪŌŖBCĶńĪŪīÔ Ĺő™y£Ĺ![]() x©Ā3£ģłýĺ›∂ĢīőļĮ żÕľŌů…ŌĶ„Ķń◊ÝĪÍŐō’ųļÕ◊ÝĪÍ”ŽÕľ–őĶń–‘÷ «ůĶ√D£®2£¨©Ā3£©£¨ňý“‘÷ĪŌŖCD°őx÷Š£ģ”…īň«ůĶ√EMĶń≥§∂»£ĽĻżĶ„F◊ųFH°ÕPM”ŕĶ„M£¨ĻĻ‘žŌŗň∆»żĹ«–ő£ļ°ųMHF°◊°ųMPQļÕ°ųCMF°◊°ųBQF£¨łýĺ›Ōŗň∆»żĹ«–őĶń∂‘”¶ĪŖ≥…Ī»ņżÕ∆÷™
x©Ā3£ģłýĺ›∂ĢīőļĮ żÕľŌů…ŌĶ„Ķń◊ÝĪÍŐō’ųļÕ◊ÝĪÍ”ŽÕľ–őĶń–‘÷ «ůĶ√D£®2£¨©Ā3£©£¨ňý“‘÷ĪŌŖCD°őx÷Š£ģ”…īň«ůĶ√EMĶń≥§∂»£ĽĻżĶ„F◊ųFH°ÕPM”ŕĶ„M£¨ĻĻ‘žŌŗň∆»żĹ«–ő£ļ°ųMHF°◊°ųMPQļÕ°ųCMF°◊°ųBQF£¨łýĺ›Ōŗň∆»żĹ«–őĶń∂‘”¶ĪŖ≥…Ī»ņżÕ∆÷™![]() £Ĺ
£Ĺ![]() £ģ…ŤMF£Ĺk£®2©Ām£©£¨QF£Ĺkm£¨”…»żĹ«–őĶń√śĽżĻę ĹļÕÕľ–őĶ√ĶĹ£ļS£ĹS°ųPQM©ĀS°ųEMF£Ĺ3©Ā
£ģ…ŤMF£Ĺk£®2©Ām£©£¨QF£Ĺkm£¨”…»żĹ«–őĶń√śĽżĻę ĹļÕÕľ–őĶ√ĶĹ£ļS£ĹS°ųPQM©ĀS°ųEMF£Ĺ3©Ā![]() £®©Ā
£®©Ā![]() m+
m+![]() £©£®2©Ām£©£Ĺ©Ā
£©£®2©Ām£©£Ĺ©Ā![]() m2+
m2+![]() m+
m+![]() £ģ
£ģ
Ĺ‚£ļ£®1£©»ÁÕľ1£¨į—Ķ„A£®©Ā2£¨0£©°ĘB£®4£¨0£©∑÷Īūīķ»Žy£Ĺax2+bx©Ā3£®a°Ŕ0£©£¨Ķ√
![]() £¨
£¨
Ĺ‚Ķ√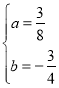 £¨
£¨
ňý“‘ł√Ň◊őÔŌŖĶńĹ‚őŲ Ĺő™£ļy£Ĺ![]() x2©Ā
x2©Ā![]() x©Ā3£Ľ
x©Ā3£Ľ

£®2£©Ĺęx£Ĺ0īķ»Žy£Ĺ![]() x2©Ā
x2©Ā![]() x©Ā3£¨Ķ√y£Ĺ©Ā3£¨
x©Ā3£¨Ķ√y£Ĺ©Ā3£¨
°ŗĶ„CĶń◊ÝĪÍő™£®0£¨©Ā3£©£¨
°ŗOC£Ĺ3£ģ
…ŤN£®x£¨y£©£¨
°ŖS°ųNAB£ĹS°ųCAB£¨
°ŗ|y|£ĹOC£Ĺ3£¨
°ŗy£Ĺ°ņ3£ģ
ĶĪy£Ĺ3 Ī£¨![]() x2©Ā
x2©Ā![]() x©Ā3£Ĺ3£¨
x©Ā3£Ĺ3£¨
Ĺ‚Ķ√x£Ĺ![]() +1£ģ
+1£ģ
ĶĪy£Ĺ©Ā3 Ī£¨![]() x2©Ā
x2©Ā![]() x©Ā3£Ĺ©Ā3£¨
x©Ā3£Ĺ©Ā3£¨
Ĺ‚Ķ√x1£Ĺ2£¨x2£Ĺ0£®…Š»•£©£ģ
◊Ř…Ōňý Ų£¨Ķ„NĶń◊ÝĪÍ «£®![]() +1£¨3£©ĽÚ£®©Ā
+1£¨3£©ĽÚ£®©Ā![]() +1£¨3£©ĽÚ£®2£¨©Ā3£©£Ľ
+1£¨3£©ĽÚ£®2£¨©Ā3£©£Ľ
£®3£©»ÁÕľ2£¨”…“—÷™Ķ√£¨QB£Ĺm£¨PQ£Ĺ2£¨
…Ť÷ĪŌŖBCĶńĪŪīÔ Ĺő™y£Ĺkx+b£®k°Ŕ0£©£ģ
°Ŗ÷ĪŌŖy£Ĺkx+bĺ≠ĻżĶ„B£®4£¨0£©£¨C£®0£¨©Ā3£©£¨
°ŗ![]() £¨
£¨
Ĺ‚Ķ√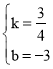 £¨
£¨
°ŗ÷ĪŌŖBCĶńĪŪīÔ Ĺő™y£Ĺ![]() x©Ā3£ģ
x©Ā3£ģ
ĶĪ0£ľm°‹2 Ī£¨”…“—÷™Ķ√PB£Ĺ2+m£ģ
°ŖOP£Ĺ2©Ām£¨
°ŗE£®2©Ām£¨©Ā![]() m©Ā
m©Ā![]() £©£ģ
£©£ģ
”…OB£Ĺ4Ķ√OP£Ĺ2£¨
į—x£Ĺ2īķ»Žy£Ĺ![]() x2©Ā
x2©Ā![]() x©Ā3÷–£¨Ķ√y£Ĺ©Ā3£¨
x©Ā3÷–£¨Ķ√y£Ĺ©Ā3£¨
°ŗD£®2£¨©Ā3£©£¨
°ŗ÷ĪŌŖCD°őx÷Š£ģ
°ŖEP£Ĺ![]() m+
m+![]() £¨MP£Ĺ3£¨
£¨MP£Ĺ3£¨
°ŗEM£ĹMP©ĀEP£Ĺ3©Ā![]() m©Ā
m©Ā![]() £Ĺ©Ā
£Ĺ©Ā![]() m+
m+![]() £ģ
£ģ
ĻżĶ„F◊ųFH°ÕPM”ŕĶ„M£¨‘Ú°ŌMHF£Ĺ°ŌMPQ£Ĺ90°„£ģ
°Ŗ°ŌHMF£Ĺ°ŌPMQ£¨
°ŗ°ųMHF°◊°ųMPQ£¨
°ŗ![]() £Ĺ
£Ĺ![]() £ģ
£ģ
°Ŗ°ŌFCM£Ĺ°ŌFBQ£¨°ŌFMC£Ĺ°ŌFQB£¨
°ŗ°ųCMF°◊°ųBQF£¨
°ŗ![]() £Ĺ
£Ĺ![]() £ģ
£ģ
°ŖCD£Ĺ2£¨
°ŗCM£Ĺ2©Ām£¨
°ŗ![]() £Ĺ
£Ĺ![]() £ģ
£ģ
…ŤMF£Ĺk£®2©Ām£©£¨QF£Ĺkm£¨
°ŗMQ£Ĺ2k£¨
°ŗ![]() £Ĺ
£Ĺ![]() £ģ
£ģ
°ŗ![]() £Ĺ
£Ĺ![]() £ģ
£ģ
°ŖPQ£Ĺ2£¨
°ŗHF£Ĺ2©Ām£ģ
°ŗS°ųEMF£Ĺ![]() EMHF£Ĺ
EMHF£Ĺ![]() £®©Ā
£®©Ā![]() m+
m+![]() £©£®2©Ām£©£ģ
£©£®2©Ām£©£ģ
°ŖS°ųPQM£Ĺ![]() PQPM£Ĺ
PQPM£Ĺ![]() °Ń3°Ń2£Ĺ3£¨
°Ń3°Ń2£Ĺ3£¨
°ŗS£ĹS°ųPQM©ĀS°ųEMF£Ĺ3©Ā![]() £®©Ā
£®©Ā![]() m+
m+![]() £©£®2©Ām£©£Ĺ©Ā
£©£®2©Ām£©£Ĺ©Ā![]() m2+
m2+![]() m+
m+![]() £ģ
£ģ

 Ņŕň„Ő‚Ņ®ľ””¶”√Ő‚ľĮ—ĶŌĶŃ–īūįł
Ņŕň„Ő‚Ņ®ľ””¶”√Ő‚ľĮ—ĶŌĶŃ–īūįł